第二種電気工事士 2019年度(上期)筆記試験の問1~10について、過去問を解説していきます
私自身、最初の問1~10問は重要だと考えています。その理由としては、毎年出題される問題が似ており解きやすいからです。特に計算問題はちょっとした違いなだけで計算方法は同じです。
それに最初の10問をすべて解くことができれば、20点獲得できることになります。つまり、残り40問に対して20問正解することができれば合格です。これは経験上ですが、資格試験の最初の問題をスムーズに解くことができると心が落ち着き焦らず試験に挑むことができます。しかし、最初の問題ができないと焦りが多くなり、単純ミスが連発しやすくなります。
ここでは、計算問題をよりかみ砕いて計算が苦手な方・電気の勉強初めてという方でもわかりやすいように解説してみましたので、ご一読ください。
それでは、どうぞ!!

2019年度 上期 問1

この問題は短絡・開放時に回路がどのようになるのかを問う問題ですね
解き方の手順は①②③の通りです。
- 手順①:問題①部分に注目し、抵抗を求める
- 手順②:問題②部分に注目し、抵抗を求める
- 手順③:電流値を求め、a-b間の電圧を求める

手順①
スイッチ(S)を閉じたとき、図1の①部分に注目してもらうと短絡状態となっています。短絡すると、0Ωと50Ωに対してどっちに電流が流れるかとなると、抵抗が無い0Ωにすべて電流が流れますよね、したがって、①は0Ωとなります。
うーん、わかりにくいなと思う方は、0Ωと50Ωが並列回路だったときを考えてみてください。合成抵抗はどうなるでしょうか。
合成抵抗 = $\frac{(0Ω×50Ω)}{(0Ω+50Ω)}$= 0Ω
したがって、①部分は0Ωになります。
手順②
次に、図2の②に注目してください、a-b間は回路が開放しているので②に電流は流れないので0Ωとなります。a-b間はスイッチを開放している状態と思ってもらえるといいかもしれません。家の照明スイッチを切っていれば照明は点灯しませんよね?それって回路が開放されているため、電流が流れていないからです。
したがって、②部分は0Ωになります。
手順③
手順①②を整理してみると、図3のように抵抗2つの直列回路となりとても簡単となります。
電流を求めてみましょう。 オームの法則より、電流I=$\frac{V}{R}$=$\frac{120}{(50+50)}$=1.2A
次に端子間abにかかる電圧Vabは、50Ωにかかる電圧のことなので、
Vab=IR=1.2A ×50Ω=60V
したがって、答えはニの60Vです
2019年度 上期 問2

この問題は許容電流を問う問題です。
許容電流とは、絶縁電線やケーブルに流すことのできる最大電流のことです。つまり、この電流以上に電流を流すと電線が発熱し、電線が溶けたり、燃えてしまいます。
電線の抵抗Rは下記の計算式になります
- R=$\frac{ρL}{A}$ (ρ:抵抗率 、L:長さ 、A:断面積 )
- 断面積とはここでいうと、円の面積の為、半径×半径×πです。整理すると、 A=$\frac{D}{2}$×$\frac{D}{2}$×π =$\frac{D^2}{4}$×π (D:直径) これを上記式に代入すると、
- R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$=$\frac{4ρL}{D^2 π}$(ρ:抵抗率 、L:長さ 、A:断面積 )
ロ、ハは上記の式により、正しいことがわかります
ニはDが大きくなると、抵抗が小さくなるので、許容電流が大きくなることがわかります
イは式にはないですが、温度上昇すると、放熱性が悪くなり、許容電流は小さくなります
したがって、答えはイです
2019年度 上半期 問3

この問題は、電力量(kW・h)を求める問題ですね
熱量と電力量の関係は ≪3600kJ=1kW・h≫ があります
水60㎏を20K上昇させる熱量は、水の比熱4.2kJ/(kg・K)により、
熱量=4.2kJ/(kg・K) ×60kg×20K =5040 kJ となります。
したがって、電力量は、5040kJ/3600 =1.4 kW・h 答えはハです
参考:ここから下は覚えたい方だけみてください
ここで、熱量の公式とか覚えてないって方は単位に注目してみましょう
ただし、熱量と電力量の関係は ≪3600kJ=1kW・h≫ 覚えといてください
kJを求めるには、問題の単位のみに注目してみると、
kJ/(kg・K)は kgとKを掛け算してしまえば、kJになることがわかります
kJ/(kg・K) × kg × K = kJ
上記の要領で数値を代入れてしまえば、答えが導けます
計算式がわからないときは、単位に注目し、計算を解くっていうのは電験三種、二種でもやるので覚えて損はないです
さらに、熱量と電力量の関係 ≪3600kJ=1kW・h≫も覚えてないという方!!
電力量1時間あたり(h)を1秒あたり(s)に変換してみてください。1時間は3600秒のため、
1kW・h=3600kW・s となります
熱量の電力量の関係は、1kJ=1kW・sなので、
1kW・h=3600kW・s=3600kJという関係がわかります
2019年度 上期 問4

まずは、インピーダンスZと電流Iを求めましょう
インピーダンスZ=$\sqrt{R^2+X^2}$=$\sqrt{8^2+6^2}$=$\sqrt{100}$=10Ω
電流I= $\frac{V}{Z}$=$\frac{100V}{10Ω}$=10A
抵抗8Ωの両端の電圧VRは、VR=電流I×抵抗R=10A×8Ω=80V
したがって、答えはニです
2019年度 上期 問5

三相交流の問題ですね。回路はΔ回路となっています
三相電力の求め方は主に下記の3パターンあります
- 三相電力P=√3×線間電圧Vℓ×線間電流Iℓ×力率cosΘ (W)
- 三相電力P=3×相電圧Vp×相電流Ip×力率cosΘ (W)
- 三相電力P=3×相電流Ip2×抵抗 (W)
それでは、求めていきましょう
Δ回路は、線間電圧Vℓ=相電圧Vp 、線電流Iℓ=√3相電流IPの関係性があります
1相のインピーダンスZは、Z=$\sqrt{R^2+X^2}$=$\sqrt{8^2+6^2}$=$\sqrt{100}$=10Ω
相電流Ipは、Ip=$\frac{相電圧Vp}{インピーダンスZ}$=$\frac{200V}{10Ω}$=20A
線電流Iℓは、Iℓ=√3×Ip=√3×20A=34.6A
力率はcosΘ=R/Z=8/10=0.8
上記結果より、三相電力は、
三相電力P=√3×線間電圧Vℓ×線間電流Iℓ×力率cosΘ (W)=√3×200V×34.6A×0.8=9577≒ 9.6kW
したがって、答えはハです
参考:他の回答方法
三相電力P=3×相電圧Vp×相電流Ip×力率cosΘ (W)、三相電力P=3×相電流Ip2×抵抗 (W) についてみてみましょう
- 三相電力P=3×相電圧Vp×相電流Ip×力率cosΘ =3×200×20×0.8=9600=9.6kW
- 三相電力P=3×相電流Ip2×抵抗=3×20^2×8=9600=9.6kW
どれも回答は一緒になりますね
2019年度 上期 問6

一見、難しい問題かと思いますが、右端から順に1つ1つ片づければ大したことありません
それでは、計算してみます
- C-C’間の抵抗は、抵抗負荷=C-C’間の電圧/C-C’間の電流=$\frac{100V}{10A}$=10Ω
- b-C-C’-b’間の抵抗は、0.1Ω+10Ω+0.1Ω=10.2Ω
- b-b’間の電圧は、Vb-b’=10.2Ω×10A=102V
- a-b間、b’-a’間の電流は、10A+5A=15A
それでは、a-b-b’-a間(a-a’間)の電圧を見ていきましょう
- a-b間の電圧は、Va-b=15A×0.1Ω=1.5V 、
- b’-a’間の電圧は Vb’-a’=15A×0.1Ω=1.5V
- a-b-b’-a’間(a-a’間)の電圧は、Va-b + Vb-b’ +Vb’-a’ = 1.5V+102V+1.5V=105V
したがって、答えは105Vのニです
2019年度 上期 問7

中性線には電流が流れていない条件となっています
Vs=rI+Vr となりますので、 Vs-Vr=rI となり、したがって、答えはハです
下の図のようなイメージしてもらえれば、分かりやすいかもしれません
どうでしょうか、ピンっと来てもらえれば!

2019年度 上期 問8

絶縁電線の許容電流についは表の通りです
表より、直径2.0mmの許容電流は35Aなので、
電線1本あたりの許容電流は、 電線1本あたりの許容電流=35A×0.56=19.6A
したがって、近い19Aとなり、答えはハです。
| 単線 | より線 | ||
| 直径(mm) | 許容電流(A) | 断面積(mm^2) | 許容電流(A) |
| 1.6 | 27 | 2 | 27 |
| 2.0 | 35 | 3.5 | 37 |
| 2,6 | 48 | 5.5 | 49 |
| 3.2 | 62 | 8 | 61 |
許容電流とは、絶縁電線やケーブルに流すことのできる最大電流のことです。つまり、この電流以上に電流を流すと電線が発熱し、電線が溶けたり、燃えてしまいます。
2019年度 上期 問9

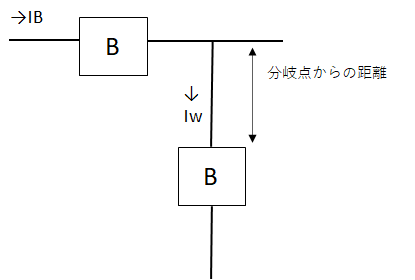
低圧屋内幹線から分岐して6mの位置とあるので、分岐点からの電線の許容電流はIwは、
Iw≧IB×0.35=100×0.35=35A (IB:幹線の過電流遮断器の定格電流)
したがって、答えは35Aのロです
参考)
分岐回路の過電流遮断器の取り付け箇所
幹線の分岐点から3m以下の箇所に過電流遮断器を設置しないといけないですが、
次の条件により3m以上の位置に取り付けできます
- 分岐点から8m以下: IW≧IB×0.35
- 任意の長さ:IW≧IB×0.55
2019年度 上期 問10

≪配線用遮断器の定格≫と≪コンセントの定格≫の条件として、
- 定格20Aの配線用遮断器を設置した分岐回路には20A以下のコンセントを使用
- 定格30Aの配線用遮断器を設置した分岐回路には20A以上~30A以下のコンセントを使用
イ、ロ、ハ、ニを見てみると、イ、ハ、ニは条件通りですが、
ロは定格30Aの配線用遮断器に対して20A以上~30A以下以外の為、誤っています。
したがって、答えはロです

お疲れさまでした。
「出典:2019年度上期 筆記試験 第ニ種電気工事士 問1~10:一般財団法人電気技術者試験センター 試験の問題と解答 | ECEE 一般財団法人電気技術者試験センター (shiken.or.jp)」
第二種電気工事士の記事の中には勉強方法を紹介しています
また、他にも電気工事士についての記事も見ていただければとおもいます


