【計算苦手な方】第二種電気工事士　2021年度（上期　午後）筆記試験　問１～１０　計算問題　過去問解説

　第二種電気工事士　2021年度（上期　午後）筆記試験の問1～10について、解説していきます

計算問題は毎年似たような問題が出てくるため、点数を取りやすいです。今回の問題も過去問と変わらない問題ばかりです。ぜひ、最初の10問を完璧に解き20点を確保しましょう。

それではどうぞ！！

2021年度（上期　午後）　問１
2021年度（上期　午後）　問2
2021年度（上期　午後）　問3
2021年度（上期　午後）　問4
2021年度（上期　午後）　問5
2021年度（上期　午後）　問6
2021年度（上期　午後）　問7
2021年度（上期　午後）　問8
2021年度（上期　午後）　問9
2021年度（上期　午後）　問10

2021年度（上期　午後）　問１

手順①：合成抵抗を求める
手順②：電流値を求める
手順③：抵抗8Ωの消費電力を求める

手順①合成抵抗を求める

まずは20Ωと30Ωの並列回路の合成抵抗は、(20Ω×30Ω)　/（20Ω+30Ω)=600Ω /50Ω＝ 12Ω

次に、12Ωと8Ωの直列回路になるので、合成抵抗は12Ω+8Ω=20Ω

手順②電流値を求める

　手順①より、合成抵抗は20Ω、電圧は200Vですので、　電流値Iは、I= 200V /20Ω =10A

手順③電抵抗8Ωの消費電力を求める

　手順②より電流値は10Aなので、抵抗8Ωの消費電力Pは、P=I^2×R=10A×10A×8Ω＝800W

したがって、答えは８００Wのロです

2021年度（上期　午後）　問2

問の直径2.6㎜、長さ20ｍの銅導線と同じ抵抗値はどれかっていう問題です。

電線の抵抗Rは下記の計算式になります

R=$\frac{ρL}{A}$　　（ρ：抵抗率　、L：長さ　、A：断面積　）
断面積Aは、円の面積の為、半径×半径×πです。　A=$\frac{D}{2}$×$\frac{D}{2}$×π＝$\frac{D^2}{4}$×π（D:直径）
R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$＝$\frac{4ρL}{D^2 π}$（ρ：抵抗率　、L：長さ　、A：断面積　）

　ここで、銅導線と銅導線を比較しているので、ρ:抵抗値は同じとなるのでρは仮で１とすると、

　R=$\frac{4ρL}{D^2 π}$＝$\frac{4×1×L}{D^2 π}$＝$\frac{4L}{D^2 π}$となるので、この式に問の数値を代入してみましょう。　　

　　R=$\frac{4L}{D^2 π}$＝$\frac{4×20m}{2.6㎜×2.6㎜×π}$=3.77Ω　　抵抗値は3.77Ωです　　

　したがって、問題中のイロハニの中から抵抗値1.88Ωに近い数値を求めろってことです。　

　イを見てみると、R=$\frac{ρL}{A}$＝$\frac{1×40ｍ}{8㎜^2}$=5Ω (ρ：１，Ｌ：40m ，Ａ：8mm²)
　ロを見てみると、R=$\frac{ρL}{A}$＝$\frac{1×20ｍ}{8㎜^2}$=2.5Ω (ρ：１，Ｌ：20m ，Ａ：8mm²)
　ハを見てみると、R=$\frac{ρL}{A}$＝$\frac{1×40ｍ}{5.5㎜^2}$=7.2Ω (ρ：１，Ｌ：40m ，Ａ：5.5mm²)
　ニを見てみると、R=$\frac{ρL}{A}$＝$\frac{1×20ｍ}{5.5㎜^2}$=3.64Ω (ρ：１，Ｌ：20m ，Ａ：5.5mm²)

したがって、3.77Ωに値が近い答えはニです

≪他の回答≫

イロハニすべてに式を代入すると面倒ですよね、そんな時にはここに注目してくだい

　問の断面積と長さに注目！！　

長さＬ：20ｍ
　断面積Ａ　：A=$\frac{D}{2}$×$\frac{D}{2}$×π =$\frac{2.6}{2}$×$\frac{2.6}{2}$×π＝5.3mm²

抵抗率は同じため、要はこれに近い値をみればいいわけです。

　イを見てみると、Ｌ：40m ，Ａ：8mm²
　ロを見てみると、Ｌ：20m ，Ａ：8mm²
　ハを見てみると、Ｌ：40m ，Ａ：5.5mm²　
　ニを見てみると、Ｌ：20m ，Ａ：5.5mm²

値が近いニが答えだとわかりますね。

したがって、答えはニです

2021年度（上期　午後）　問3

熱量と電力量の関係は　≪3600kJ=1kW・h≫ があります

消費電力Pは400W、1時間20分使用したの電力量Wを求めると、

　W＝P×t =400W×(80分/60分）h＝400W× 1.33h=533Wh

電力量は1時間あたりなので、秒に変換すると、1時間は3600秒となりますので

熱量と電力量の関係は　≪3600kJ=3600ｋＷ・ｓ＝1kW・h≫より、

熱量は、　Q＝W×t=533×3600＝1,918,800J＝1919kJ　

したがって、答えは1920kJのロです。

2021年度（上期　午後）　問4

抵抗、リアクタンス、全体に流れている電流値は問に記入されている為、求めやすいです。

力率cosθは、回路全体に流れる電流Iと抵抗に流れる電流IRによって求められます。

cosθ=$\frac{IR}{I}$=$\frac{6A}{10A}$ =0.6　×100％＝60%

したがって、答えはロです

2021年度（上期　午後）　問5

　三相交流の問題ですね。回路はY（スター）回路となっています。

スター回路は、線間電圧Vℓ＝√3×相電圧V　、線電流Iℓ＝相電流I($\frac{相電圧}{抵抗}$)　の関係があります

相電圧V=$\frac{線間電圧Vℓ}{√3}$ ＝$\frac{200V}{√3}$＝115.6V

相電流I=$\frac{相電圧}{抵抗}$=$\frac{115.6V}{20Ω}$ =5.78A

したがって、答えはハです。

2021年度（上期　午後）　問6

一見、難しい問題かと思いますが、右端から順に１つ１つ片づければ簡単です。

それでは、計算してみます

　c-c’間の抵抗は、抵抗負荷＝$\frac{c-c’間の電圧Vc-c’}{c-c’間の電流Ic-c’}$＝$\frac{100V}{5A}$＝2０Ω
　b-c-c’-b’間の抵抗は、Rb-c-c’-b’=0.1Ω+2０Ω+0.1Ω＝20.2Ω
　b-b’間の電圧は、Vb-b’=20.2Ω×5Ａ＝101Ｖ
　a-b間、ｂ’-a’間の電流Ia-b=Iｂ’-a’は、Ia-b=Ib-c+Ib-b’=5A+5A=10A

それでは、a-b-ｂ’-a間（a-a’間）の電圧を見ていきましょう

a-b間の電圧は、Va-b=10A×0.05Ω＝0.5V　、
ｂ’-a’間の電圧は　Vｂ’-a’=10A×0.05Ω＝0.5V　
a-b-ｂ’-a’間（a-a’間）の電圧は、Va-b + Vb-b’ +Vｂ’-a’ = 0.5V+101V+0.5V=102V

したがって、答えは102Vのロです

2021年度（上期　午後）　問7

中性線が断線してるので、ただの電圧200Vと100Ω、50Ωの直列回路となります。

電流値Iを求めると、I=$\frac{200V}{150Ω}$=1.33Aです

a-b間の電圧Vabとは、100Ωの両端の電圧のことなので、

Vab＝電流I×100Ω＝1.33A×100Ω＝133V

　したがって、答えはハです

2021年度（上期　午後）　問8

絶縁電線の許容電流についは表の通りです

表より、直径1.6mmの許容電流は27Ａなので、

電線1本あたりの許容電流は、　電線1本あたりの許容電流＝27A×0.56=15.1A

したがって、答えはイです。

単線		より線
直径(mm)	許容電流（A)	断面積（mm²)	許容電流（A)
1.6	27	2	27
2.0	35	3.5	37
2,6	48	5.5	49
3.2	62	8	61

許容電流とは、絶縁電線やケーブルに流すことのできる最大電流のことです。つまり、この電流以上に電流を流すと電線が発熱し、電線が溶けたり、燃えてしまいます。

2021年度（上期　午後）　問9

分岐回路の過電流遮断器の取り付け箇所の条件は、下記3通りです。

幹線の分岐点から３ｍ以下の箇所に過電流遮断器を設置しないといけないですが、　　　　　　　　　　　　　　　　　次の条件により3m以上の位置に取り付けできます
3ｍ以上～8ｍ以下：IW≧IB×0.35　（Iw：電線の許容電流、IB:幹線の過電流遮断器の定格電流）
８m以上：IW≧IB×0.55

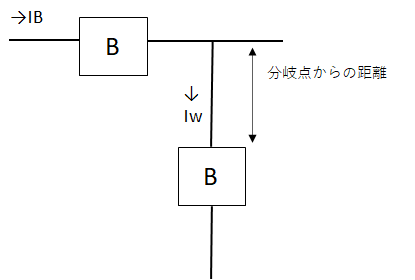
イ、ロは、幹線の分岐点からL=３ｍ以下なので適切

ハは、L=10mなので、８m以上：IW≧IB×0.55の条件となります。　　　　　　　　　　　　　　　　　　　　幹線の過電流遮断器の定格電流IBの55%以上でなければいけません。　　　　　　　　　　　　　　　　　　　　　　　　　つまり、IB=100なので、許容電流Iw=55A以上となります。問では42Aなので不適切　　

ニは、L=15mなので、８m以上：IW≧IB×0.55の条件となります。　　　　　　　　　　　　　　　　　　　　幹線の過電流遮断器の定格電流IBの55%以上でなければいけません。　　　　　　　　　　　　　　　　　　　　　　　　　つまり、IB=100なので、許容電流Iw=55A以上となります。問では61Aなので適切

したがって、答えはハです

2021年度（上期　午後）　問10

≪配線用遮断器の定格≫と≪コンセントの定格≫、≪電線の太さ≫の条件として、

下記表を参照

分岐回路	コンセント	電線の太さ
15A	15A以下	1.6㎜以上
20A 配線用遮断器	20A以下	1.6mm以上
20A ヒューズ	20A	2.0mm以上
30A	20～30A	2.6mm以上断面積5.5mm²以上
40A	30～40A	断面積8.0mm²以上
50A	40～50A	断面積14.0mm²以上