【計算苦手な方】第1種電気工事士　2018年度 筆記試験　問1～11,16　過去問解説

　第1種電気工事士　2018年度 筆記試験の問1～11、16について、解説していきます

計算問題は毎年似たような問題が出てくるため、点数を取りやすいです。今回の問題も過去問と変わらない問題ばかりです。

それではどうぞ！！

2018年度　問１

１．コンデンサC‎に蓄えられるエネルギーWc

　エネルギーWcは、Wc＝$\frac{1}{2}$ CV²で求めることができます。

コンデンサC＝20×10^-6 【F】（20【μF】=20×10^-6 【F】　μは1×10^-6) 、コンデンサ両端に掛かる電圧Vは100【V】

エネルギーWcは、Wc＝$\frac{1}{2}$CV²に代入すると、Wc＝$\frac{1}{2}$×20×10^-6×100² =0.1【J】

２．リアクトルLに蓄えられるエネルギーW_L

　エネルギーW_Lは、W_L＝$\frac{1}{2}$ LI²で求めることができます。

リアクトルL=2×10^-3 【mH】(2【mH】=2×10^-3 【H】mは1×10^-3) 、リアクトルに流れる電流Iは10【A】

エネルギーW_Lは、W_L＝$\frac{1}{2}$ LI²に代入すると、W_L＝$\frac{1}{2}$×2×10^-3×10² =0.1【J】

したがって、答えはハです

2018年度　問2

問題を解くのに上記図として問題を解いていきます。

1 直列・並列負荷に掛かる電圧を求める

≪回路の電圧について電源電圧は72V≫

直列の2Ωに流れる電流は20Aの為、2Ωにかかる電圧は40Vとなります。

並列回路(2Ω、10Ω、R)にかかる電圧は残りの32V（72V-40V）となります。

2　電流I_Rを求める

回路の電流について、合計電流はI1+I2+I_R=20A
2Ωに流れる電流I1は、I1=V/2Ω＝$\frac{32V}{2Ω}$=16A
10Ωに流れる電流I2は、I2=V/10Ω＝$\frac{32V}{10Ω}$=3.2A

抵抗Rに流れる電流I_R=20A – I1 – I2=20A – 16A – 3.2A =0.8A

したがって、答えはイです

2018年度　問3

　電流の瞬時値iは v/XL=にて求めることができます。

交流電圧v、リアクタンスXLは、問より、v=100√2sin(2πft)、リアクタンスXL=10Ω です。これを式に代入すると、

i=$\frac{v}{XL}$=$\frac{100√2sin(2πft)}{10Ω}$/10＝10√2sin(2πft-90°）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　※リアクタンスは電圧に対して電流の位相を90°遅らせる作用があるのでマイナス90°が付きます。

参考：
コンデンサは、電圧に対して電流の位相を90°（π/2)進ませます。
i=v/XL=100√2sin(2πft)/10Ω=10√2sin(2πft+90°）※プラスがつくと進みという意味になります。

したがって、答えはイです。

2018年度　問4

1　抵抗Rを求める

　抵抗Rを求めるには、抵抗Rでの消費電力800W、電流10Aによって求めることができます。

消費電力Pの公式は、P=I²×Rなので、式をR＝の形に変更すると、R=$\frac{P}{I^2}$＝$\frac{800W}{10A^2}$=8Ω

2　インピーダンスZを求める

インピーダンスZは、Z=$\sqrt{R^2+X^2}$で求めることができます。
リアクタンスXは、X=XL-XC=16Ωー10Ω= ６Ω

したがって、インピーダンスZは、Z=$\sqrt{R^2+X^2}$=$\sqrt{8^2+6^2}$=$\sqrt{100}$=10Ω

3　電源電圧Vを求める

電源電圧Vは、インピーダンスZと電流Iで求めることができます。

電源電圧V=IZ=10A×10Ω＝100V

したがって、答えはロです

2018年度　問5

1 Y回路の線電流を求める

　Y回路は線間電圧V＝√3×相電圧V　、線電流I＝相電流Iの関係があるのでこれを基に下記を求める

1. 相電圧を求める：相電圧＝$\frac{線間電圧V}{√3}$
2. 相電流を求める：相電流＝$\frac{相電圧}{抵抗R}$ ＝$\frac{ V}{√3×R}$
3. 線電流を求める：線電流＝相電流なので、線電流=$\frac{ V}{√3×R}$

2 Δ回路の線電流を求める

　Δ回路は線間電圧V＝相電圧V　、線電流I＝√3相電流Iの関係があるのでこれを基に下記を求める

1. 相電圧を求める：線間電圧＝相電圧なので、V
2. 相電流を求める：相電流＝$\frac{相電圧}{抵抗R}$＝$\frac{V}{R}$
3. 線電流を求める：線電流＝√3×相電流＝√3$\frac{ V}{R}$

3 Y回路とΔ回路の線電流を合計する

≪Y回路の線電流は$\frac{ V}{√3×R}$≫、≪Δ回路の線電流は√3$\frac{ V}{R}$≫なので、合計値は、

　$\frac{ V}{√3×R}$＋√3$\frac{ V}{R}$　＝√3$\frac{ V}{R}$×（$\frac{ 1}{√3}$+√3）

したがって、答えはハです。

2018年度　問6

問の図だとわかりにくいので下記の図を参考していただければと思います。

1　電流値を求める

各負荷に流れる電流は、下記の通りです。

• 負荷Aに流れる電流IAは10A
• 負荷Bに流れる電流IBは5A
• 負荷Cに流れる電流ICは5A

真ん中の0.5Ωに流れる電流I2とすると、I2= IB ＋ IC = 5A + 5A =10A

真ん中の0.5Ωに流れる電流I1とすると、I1= I2 ＋ IA = 10A + 10A =20A

2　抵抗Aに掛かる電圧VAを求める

　VAを求めるには、電源電圧 210V – 電圧降下分(0.1Ω×I1＋0.1Ω×I1）で求められます。

　VA = 210V – 0.1Ω×I1 – 0.1Ω×I1 = 210V – 0.1Ω×20A- 0.1Ω×20A = 206V

3　抵抗Bに掛かる電圧VBを求める

　VBを求めるには、VA – 電圧降下分(0.1Ω×I2＋0.1Ω×I2）で求められます。

　VB = VA – 0.1Ω×I2 – 0.1Ω×I2= 206V – 0.1Ω×10A- 0.1Ω×10A = 204V

4　抵抗Cに掛かる電圧VCを求める

　VCを求めるには、VB- 電圧降下分(0.1Ω×IC＋0.1Ω×IC）で求められます。

　VC = VB – 0.1Ω×IC – 0.1Ω×IC= 204V – 0.1Ω×5A- 0.1Ω×5A = 203V

したがって、答えはロです

【別解】

回路全体の電圧降下分を求め、電源電圧から差し引いてもVCを求めれることができます。

電源電圧210V – 0.1Ω×I1 – 0.1Ω×I1 – 0.1Ω×I2 – 0.1Ω×I2 – 0.1Ω×IC – 0.1Ω×IC =210-2-2-1-1-0.5-0.5=203V

2018年度　問7

この問題はめっちゃ難易度が高いです。電験三種で勉強する内容なので飛ばしても問題ないです。興味のある方だけ解いてみてください。

1　IAを複素数に変換

　電流IA＝10 A (力率cos0.5 遅れ）を複素数へ変換の為、sinθを求める

1=$\sqrt{cos^2θ1+sin^2θ1}$より、sinθ1=$\sqrt{1-cos^2θ1}$= $\sqrt{1-0.5^2}$=$\sqrt{0.75}$＝ =0.5√3 となります。

電流IAを複素数へ変換すると、IA= I（cosθ + jsinθ)　＝　10A (0.5 – j0.5√3)＝5 – j5√3 【A】　　　　　※遅れ負荷の為、- j5√3となります。　　　　　　　

2　中性線の電流IN = IA- IBにて求める

IBは力率100%の為、sinθは0なので、IBを複素数へ変換すると IB=10A

　IN＝IA-IB＝5 – j5√3 – 10=5-10- j5√3＝-5- j5√3　【A】

INを複素数から大きさへ変換すると、IN=$\sqrt{(-5)^2+( j5√3)^2}$=√100＝10 A

　したがって、答えはロです

2018年度　問8

公式の暗記問題となっています。それぞれの公式を見ていきましょう

上記公式より、イがP_L  ＝ √3 rI²なので、P_L  ＝ 3 rI²と異なるので誤りとなります。

したがって、答えはイです。

2018年度　問9

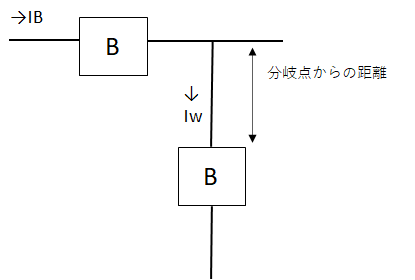
幹線の遮断器の定格電流IBは、IB=100Ａですので、それぞれの条件を見てみると、

• 3ｍ以上～8ｍ以下：IW≧IB×0.35≧100×0.35 ≧35A
• 8ｍ以上：IW≧IB×0.55 ≧ 100×0.55≧55A

イは、分岐から4m、IW=34Ａなので、≪条件3～8m以内の為、IWは35A以上なので不適切≫

ロは、分岐から5m、IW=42Ａなので、≪条件3～8m以内の為、IWは35A以上をクリア≫

ハは、分岐から９m、IW=61Ａなので、≪条件3～8m以内の為、IWは55A以上なのでクリア≫

ニは、2つ条件があります

• 条件①：分岐から6m、IW=42Ａなので、≪条件3～8m以内の為、IWは35A以上なのでクリア≫ 　
• 条件②：分岐から1m、≪3m以内に遮断器を設置しているのでクリア≫

二は非常にわかりずらい問題となっています。

したがって、答えはイです

2018年度　問10

回転速度の公式は　N＝$\frac{120f}{p}$×(1−s)【min^-1】より、一次周波数f= の形に変換すると、

f=$\frac{N×p}{120×（1-s）}$この式に回転速度1140min^-1　極数p=6　滑りs=0.05 を代入すると、

f=$\frac{N×p}{120×（1-s）}$＝$\frac{1140×6}{120×（1-0.05）}$＝60Hz

したがって、答えはニです。

2018年度　問11

これは公式なので覚えるしかないです。

電動機の出力Pは、P=100W× $\frac{v}{n}$ 【kW】 (W：巻上荷重【kN】, v：速度【m/s】, 巻上機の効率n:【%】

したがって、答えはイです

2018年度　問16

水力発電所の発電機出力【kW】の公式は、P= 9.8QHn  なので、Q：20 m³ / s　H：100ｍ　n： 0.85を代入すると、

P= 9.8QHn＝9.8×20×100×0.85＝16,660 kW= 16.7 MW　

したがって、答えはハです。

以上、お疲れさまでした。

「出典：2018年度　筆記試験　第1種電気工事士　問1～11、16　:一般財団法人電気技術者試験センター 試験の問題と解答 | ECEE 一般財団法人電気技術者試験センター (shiken.or.jp)　」