【計算問題苦手な方必見】第二種電気工事士　2020年度下期（午後　筆記試験　過去問　解説

　第二種電気工事士　2020年度（下期　午後）筆記試験の問1～10について、過去問を解説していきます

計算問題は毎年似たような問題が出てくるため、点数を稼ぎやすいです。他のサイトでは、計算問題は後回しにして他の暗記問題を解いてと見かけますが、個人的には暗記するより簡単な計算な問題で点数を稼いだ方がいいかなって思います。

計算問題の過程を飛ばさずに解説していきますので、より理解が深めていただければと思います。

それでは、どうぞ！！

２０２０年度　下期（午後）　問１
２０２０年度　下期（午後）　問2
２０２０年度　下期（午後）　問3
２０２０年度　下期（午後）　問4
２０２０年度　下期（午後）　問5
２０２０年度　下期（午後）　問6
２０２０年度　下期（午後）　問7
２０２０年度　下期（午後）　問8
２０２０年度　下期（午後）　問9
２０２０年度　下期（午後）　問10

２０２０年度　下期（午後）　問１

　一見、見たことない回路で難しく感じますよね？ただ、計算の手順としてはオームの法則を知っていれば解くことができます。基本的には与えられた数値とオームの法則で解くことができるので特殊なことは特に何もしません。計算手順を解説します

手順①：電流値を求める
手順②：回路のa-b間を短絡して、回路を上または下で分け電圧を求める

えっ！！と思うかもしれませんが、たった２つの手順で解くことができます。詳しく見ていきましょう

手順①電流値を求める

　　電圧Vは100Vと100Vなので計２００Vですね、抵抗Rは20Ωと30Ωの直列接続なので50Ωです。

　　電流Iはオームの法則より、I=$\frac{V}{R}$なので、I＝$\frac{200V}{50Ω}$＝４A

手順②回路のa-b間を短絡して回路を上又は下で分け電圧を求める

　上図のようにa-b間を短絡して回路わけてみると、上回路は図(a)、下回路は図(b)となります。こう見れば簡単な見慣れた回路ですよね。

図(a)で電圧を求めてみると、電流は手順①より４Aなので、20Ωにかかる電圧は4A×20Ω＝80Vとなります。

したがって、a-b間の電圧は、100V-80V＝20Vとなります。

したがって、答えはロの20Vです

念のため、図(b)でも同様に確認すると、30Ωにかかる電圧は4A×30Ω＝120Vとなります。

したがって、a-b間の電圧は、100V-120V＝-20Vとなります。

ここでマイナスがついて、間違えているんじゃないか不安になっちゃいますよね。

ただ、特に気にしなくても大丈夫です！！安心してください！マイナスの場合、電流が逆方向に流れているということです。ここの回路では、電流は時計回りに流れていますが、図(b)は電流が半時計周りに流れているということです。

２０２０年度　下期（午後）　問2

電線の抵抗Rは下記の計算式になります

R=$\frac{ρL}{A}$　　（ρ：抵抗率　、L：長さ　、A：断面積　）
断面積とはここでいうと、円の面積の為、半径×半径×πです。整理すると、　　　　　　　　A=$\frac{D}{2}$×$\frac{D}{2}$×π　＝$\frac{D^2}{4}$×π　　（D:直径）　　これを上記式に代入すると、
R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$＝$\frac{4ρL}{D^2 π}$（ρ：抵抗率　、L：長さ　、A：断面積　）

上記抵抗の式ですが、抵抗A,Bの比較の為、長さL、直径D のみに注目してみとR=$\frac{L}{D^2}$となります。したがって、抵抗RA,RBに数値を代入すると、

抵抗RA=$\frac{L}{D^2}$=$\frac{100}{1.6^2}$=39.06
抵抗RB=$\frac{L}{D^2}$=$\frac{50}{3.2^2}$=4.88

抵抗RAは抵抗RBの何倍でしょうか。　

　　　抵抗RA/抵抗RB=$\frac{39.06}{4.88}$ =8.00

したがって、答えは8のニです

２０２０年度　下期（午後）　問3

熱量と電力量の関係は　≪3600kJ=1kW・h≫ があります

電力を求めると、　　P＝I²×R＝10A×10A×0.2Ω＝20 W

次に、1時間あたりの電力量を求めると、W＝P×t =20W×１ｈ＝20Wh

電力量は1時間あたりなので、秒に変換すると、1時間は3600秒となりますので

熱量と電力量の関係は　≪3600kJ=3600ｋＷ・ｓ＝1kW・h≫より、

熱量は、　Q＝W×t=２０×3600＝72000J＝72kJ　

したがって、答えは72kJのイです。

２０２０年度　下期（午後）　問4

直列回路で力率を求めるには　下記の通りです

力率cosθ＝　$\frac{R}{Z}$＝$\frac{R}{\sqrt{R^2+X^2}}$　
力率cosθ＝　$\frac{VR}{V}$　　VR:抵抗の両端の電圧

　下の式に代入すると、力率cosθ＝　$\frac{VR}{V}$　＝$\frac{180V}{204V}$　＝0.88　→　88％

したがって、答えはニです

２０２０年度　下期（午後）　問5

　三相交流の問題ですね。回路はY（スター）回路となっています。

スター回路は、線間電圧Vℓ＝√3×相電圧Vp　、線電流Iℓ＝相電流Ip　の関係があります

相電圧Vｐ：抵抗両端の電圧（黄色枠部分）　　線間電圧Vℓ：線と線の間の電圧（赤枠部分）

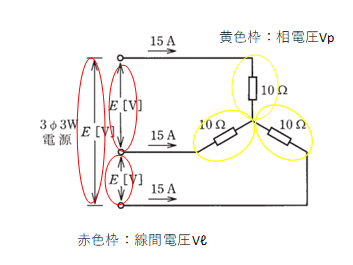
まずは、相電圧Vpを求めましょう。Vp=Ip×R＝15A×10Ω＝150V

次に線間電圧Vℓは、Vℓ＝√3×Vpより、Vℓ＝√3×150V＝　259.8V＝260V

したがって、答えは260Vのハです。

参考：Δ回路について

　Δ回路の線間電圧と相電圧、線電流と相電流の関係性は、下記の通りです。

　Δ回路は、線間電圧Vℓ＝相電圧Vp　、線電流Iℓ＝√3相電流IP

２０２０年度　下期（午後）　問6

　解答の手順は下記通り求めましょう

手順①：電流を求める
手順②：抵抗を求める
手順③：電圧降下を求める

手順①：電流を求める

　電力Pは、P=電圧V×電流Iで求められるため、式を変換し電流Iを求めると、
　電流I=$\frac{電力P}{電圧V}$=$\frac{1600W}{100V}$=16A

手順②：抵抗値を求める

　　電線の電気抵抗は1000ｍあたり5.0Ωなので、
　　12ｍの電線の電気抵抗は、5Ω×12ｍ/1000ｍ　＝0.06Ω

手順①②をまとめてみると下記の図に変換できます。　

手順③：電圧降下を求める

　電圧降下は0.06Ωの両端の電圧値となります、つまり、V=IR＝16A×0.06Ω＝0.96V　
　回路図をみると、上下2か所に0.06Ωはあるので、2倍の2×0.96V＝1.92V
　電圧降下は1.92V

したがって、答えは２のロです

　手順①～③をまとめると回路は下記のようになります。電源電圧は101.92Vとなることがわかります。つまり、電線の抵抗によって、抵抗負荷までの間に100Vに減ってしまうことを電圧降下といいます。

２０２０年度　下期（午後）　問7

　問題を見ると、右上・右下の抵抗負荷に２0A流れていることがわかります。ということは、つまり中性線には電流が流れていないこととなり、下記の図になります

　この回路の電線路の電力損失Ｐは、P=I²×r＋I²2×r＝2I²×rとなるので、

　Ｐ＝２×I²×r＝2×20Ａ×20Ａ×0.1＝80（Ｗ）

　したがって、答えはハです

２０２０年度　下期（午後）　問8

絶縁電線の許容電流についは表の通りです

表より、断面積3.5mm²の許容電流は３7Ａなので、

電線1本あたりの許容電流は、　電線1本あたりの許容電流＝37A×0.63=23.3A

したがって、近い23Aとなり、答えはロです。

単線		より線
直径(mm)	許容電流（A)	断面積（mm²)	許容電流（A)
1.6	27	2	27
2.0	35	3.5	37
2,6	48	5.5	49
3.2	62	8	61

許容電流とは、絶縁電線やケーブルに流すことのできる最大電流のことです。つまり、この電流以上に電流を流すと電線が発熱し、電線が溶けたり、燃えてしまいます。

２０２０年度　下期（午後）　問9

許容電流Iwを求める問題ですね。Iｗを求めるには下の表を使って求めます

表.許容電流を求める条件
※IM:電動機の定格電流　　、　その他負荷の定格容量IH

電動機５台の定格電流の合計は需要率が80％なので定格電流IMは、

IM=12A×5台×0.8＝48A　　※その他負荷は無いのでIH=０

表より、条件②が該当し、IM≦50A以下なので、許容電流Iwは、1.25IMとなることがわかります。

したがって、Iw=1.25×48A＝６０A

答えは60Aのロです

２０２０年度　下期（午後）　問10

≪配線用遮断器の定格≫と≪コンセントの定格≫、≪電線の太さ≫の条件として、

下記表を参照

分岐回路	コンセント	電線の太さ
15A	15A以下	1.6㎜以上
20A 配線用遮断器	20A以下	1.6mm以上
20A ヒューズ	20A	2.0mm以上
30A	20～30A	2.6mm以上断面積5.5mm²以上
40A	30～40A	断面積8.0mm²以上
50A	40～50A	断面積14.0mm²以上