第二種電気工事士 2017年度(下期) 筆記試験の問1~10について、解説していきます
計算問題は毎年似たような問題が出てくるため、点数を取りやすいです。今回の問題も過去問と変わらない問題ばかりです。ぜひ、最初の10問を完璧に解き20点を確保しましょう。
それではどうぞ!!
2017年度(下期) 問1

1 電流を求める
2 回路のa-b間を短絡して、回路を上または下で分け電圧を求める
一見、見たことない回路で難しく感じますよね?ただ、計算の手順としてはオームの法則を知っていれば解くことができます。基本的には与えられた数値とオームの法則で解くことができるので特殊なことは特に何もしません。計算手順を解説します
1. 電流を求める
電流Iはオームの法則より、I=$\frac{V}{R}$なので、I=$\frac{100V+100A}{40Ω+60Ω}$=2A
2. 回路のa-b間を短絡して、回路を上または下で分け電圧を求める

上図のようにa-b間を短絡して回路わけてみると、上回路は図1、下回路は図2となります。
図1で電圧を求めてみると、1.より電流は2Aなので、40Ωにかかる電圧は、2A×40Ω=80Vとなります。
したがって、a-b間の電圧Vabは、Vab=100V-80V=20Vとなります。
したがって、答えはイです
念のため、図2でも同様に確認すると、60Ωにかかる電圧は2A×60Ω=120Vとなります。
したがって、a-b間の電圧は、100V-120V=-20Vとなります。マイナスとなっていますが、電流の向きが反対との意味となります。
2017年度(下期) 問2

1 インピーダンスZを求める
2 回路全体に流れる電流Iを求める
3 抵抗8Ωに掛かる電圧を求める
1. インピーダンスZを求める
抵抗8Ωとリアクタンス6Ωの直列回路なので、インピーダンスZは、
Z=$\sqrt{R^2+X^2}$=$\sqrt{8^2 +6^2 }$=$\sqrt{100}$=10Ω
2. 回路全体に流れる電流Iを求める
電源電圧100V、インピーダンス10Ωより、電流Iは、
I=$\frac{V}{Z}$=$\frac{100V}{10Ω}$=10A
3. 抵抗12Ωに掛かる電圧Vrを求める
抵抗8Ωと回路に流れる電流Iによって、オームの法則より12Ωに掛かる電圧Vrは求められますので、
Vr=8Ω×10A=80V
したがって、答えはニです
2017年度(下期) 問3

電線の抵抗Rは下記の式によって、求められる
R=$\frac{ρL}{A}$ (ρ:抵抗率 、L:長さ 、A:断面積 )
※断面積Aは、円の面積の為、半径×半径×πです。 A=$\frac{D}{2}$×$\frac{D}{2}$×π=$\frac{D^2}{4}$×π(D:直径)
R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$=$\frac{4ρL}{D^2 π}$
電線の抵抗Rは下記の計算式となります。
- R=$\frac{ρL}{A}$ (ρ:抵抗率 、L:長さ 、A:断面積 )
- 断面積Aは、円の面積の為、半径×半径×πです。 A=$\frac{D}{2}$×$\frac{D}{2}$×π=$\frac{D^2}{4}$×π(D:直径)
- R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$=$\frac{4ρL}{D^2 π}$(ρ:抵抗率 、L:長さ 、A:断面積 )
したがって、答えはロです。
2017年度(下期) 問4

1 電力量Wを求める
2 熱量Qを求める
≪ポイント≫
電力量Wと熱量Qはそれぞれ下記の計算式となります
電力量W:W=P×t (kW・h) 【P:消費電力 (kW)、t:時間(h)】
熱量Q:Q= c×m×T(kJ) 【c:比熱 (kJ/(kg・K) )、m:質量(kg)、T:温度変化(K)】
熱量Qと電力量Wの関係性 ≪3600kJ=1kW・h≫ ※ Q=3600×W W=Q / 3600によってそれぞれ求められる
1. 電力量Wを求める
電力量Wは、電力量W=P×t より、W=P×t =400W ×80/60 h=533.3W・h=0.5333kW ・h となります
2. 熱量Qを求める
熱量Qと電力量Wの関係性 ≪3600kJ=1kW・h≫ より、 熱量Q=3600×Wによって求められるので、電力量をを代入すると、
熱量Q=3600×W=3600× 0.5333kWh=1920kJ となります 。
したがって、答えはロです
2017年度(下期) 問5

1 インピーダンスZを求める
2 相電流Iを求める
3 消費電力Pを求める
【ポイント】
Δ回路は、線間電圧E=相電圧V 、線電流I=√3×相電流I の関係があります
相電圧V:抵抗両端の電圧(赤枠部分) 線間電圧E:線と線の間の電圧(黄色部分)

三相電力の求め方は主に下記の3パターンあります
- 三相電力P=√3×線間電圧Vℓ×線間電流Iℓ×力率cosΘ (W)
- 三相電力P=3×相電圧Vp×相電流Ip×力率cosΘ (W)
- 三相電力P=3×相電流Ip2×抵抗 (W)
1 インピーダンスZを求める
1相当たりのインピーダンスZは、抵抗6Ωとリアクタンス8Ωの直列回路なので、インピーダンスZは、
Z=$\sqrt{R^2+X^2}$=$\sqrt{6^2 +8^2 }$=$\sqrt{100}$=10Ω
2 相電流をを求める
線間電圧E=相電圧Vなので、相電圧は200V、
相電流は、相電流I= $\frac{相電圧V}{インピーダンスZ}$= $\frac{200V}{10Ω}$=20A となります。
3 消費電力Pを求める
消費電力Pは何通りかで求めることができますが、力率を使用しない 3×相電流Ip2×抵抗 (W) を使って求めます。
消費電力P= 3×相電流I2×抵抗 =3× 20A2×6Ω= 7200W =7.2kWとなります。
したがって、答えはハです。
2017年度(下期) 問6

1 配線における電圧降下を求める
1. 配電における電圧降下を求める

電線の抵抗は長さ1m当たりrΩなので、長さL mでの抵抗は、rLとなります。
rL部分の電圧vは、v=抵抗rL×電流I=rL×10A=10rLとなります。
電源電圧V1は、図の黄色部分の電圧となりますので、V1=V2+v+v=V2+10rL+10rL =V2+20rLなので、
配線の電圧降下V1-V2は、V1-V2=20rL となります。
したがって、答えはニです
2017年度(下期) 問7

絶縁電線の許容電流についは表の通りです
表より、直径1.6mmの許容電流は27Aなので、
電線1本あたりの許容電流は、電線1本あたりの許容電流=27A×0.56=15.1A
したがって、答えはイです
| 単線 | より線 | ||
| 直径(mm) | 許容電流(A) | 断面積(mm2) | 許容電流(A) |
| 1.6 | 27 | 2 | 27 |
| 2.0 | 35 | 3.5 | 37 |
| 2,6 | 48 | 5.5 | 49 |
| 3.2 | 62 | 8 | 61 |
許容電流とは、絶縁電線やケーブルに流すことのできる最大電流のことです。つまり、この電流以上に電流を流すと電線が発熱し、電線が溶けたり、燃えてしまいます。
2017年度(下期) 問8

電線の許容電流Iwを求める問題 です。
条件としては下記の通りです※IM:電動機の定格電流、その他負荷の定格容量IH

- 電動機の定格電流:IM=10A
- その他負荷の定格容量:IH=15A+20A =35A
上記1.2.より、IM≦IHなので、条件①となりますので、許容電流Iwは、
許容電流Iw=IM+IH=10A+35A=45A となります。
したがって、答えはイです。
2017年度(下期) 問9

≪配線用遮断器の定格≫と≪コンセントの定格≫、≪電線の太さ≫の条件として、
下記表を参照
| 分岐回路 | コンセント | 電線の太さ |
| 15A | 15A以下 | 1.6㎜以上 |
| 20A 配線用遮断器 | 20A以下 | 1.6mm以上 |
| 20A ヒューズ | 20A | 2.0mm以上 |
| 30A | 20~30A |
2.6mm以上 断面積5.5mm2以上 |
| 40A | 30~40A | 断面積8.0mm2以上 |
| 50A | 40~50A | 断面積14.0mm2以上 |
それぞれ条件を見てみると、
- イは分岐回路20Aに対して、定格電流30Aコンセントなので不適切
- ロは分岐回路30Aに対して、電線の太さ2.0mmなので不適切
- ハは分岐回路20Aに対して、定格電流20Aコンセント、電線の太さ2.0mmなので適切
- ニは分岐回路30Aに対して、定格電流15Aコンセントなので不適切
したがって、答えはハです
2017年度(下期) 問10

【分岐回路の過電流遮断器の取り付け箇所の条件】は、下記3通りです。
- 幹線の分岐点から3m以下の箇所に過電流遮断器を設置しないといけないですが、次の2,3の条件により3m以上の位置に取り付けできます
- 3m以上~8m以下:IW≧IB×0.35 (Iw:電線の許容電流、IB:幹線の過電流遮断器の定格電流)
- 8m以上:IW≧IB×0.55
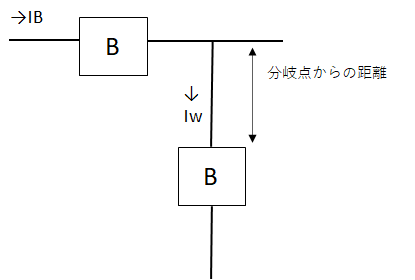
VVRケーブル太さ5.5mm2 の許容電流IWは34A、過電流継電器の定格電流IBは100Aと与えられています。
$\frac{ VVRケーブル太さ5.5mm^2の許容電流 IW }{ 過電流継電器の定格電流IB }$=$\frac{34A}{100A}$=0.34 となります。
過電流継電器の取付条件を見てみると、0.35以下の0.34なので、条件1に当てはまるので3m以下です。
したがって、答えはイです
以上、お疲れさまでした。
「出典:2017年度下期筆記試験 第ニ種電気工事士 問1~10:一般財団法人電気技術者試験センター 試験の問題と解答 | ECEE 一般財団法人電気技術者試験センター (shiken.or.jp)」


