【計算が苦手な方】電工2種　2019年下期　筆記試験　問1～10解説

　第二種電気工事士　2019年度（下期）筆記試験の問1～10について、過去問を解説していきます

　筆記試験では、前半の10問目くらいまでに計算問題が出題されることが多く、計算が苦手が方は過去問やると計算問題でつまずきやる気でないって方は多いのではないでしょうか。

　計算問題は毎年似たような問題が出てくるため、点数を稼ぎやすく合格へは欠かせない分野です。ここでは、計算過程や重要なポイントは表などにまとめて解説しますので、今より計算問題への理解を深め合格へ近づいていただければなと思います。

それでは、どうぞ！！

２０１９年度　下期　問１
２０１９年度　下期　問2
２０１９年度　下期　問3
２０１９年度　下期　問4
２０１９年度　下期　問5
２０１９年度　下期　問6
２０１９年度　下期　問7
２０１９年度　下期　問8
２０１９年度　下期　問9
２０１９年度　下期　問10

２０１９年度　下期　問１

　　並列回路の中にさらに並列回路があって、ぱっと見は構えてしまいますが、解答手順としては簡単です。

手順①：図１の黄色の直並列回路の合成抵抗を求める
手順②：図３の並列回路の合成抵抗を求める

手順①直並列回路の合成抵抗を求める

　　まずは図１の黄色部分の直並列回路の並列部分の合成抵抗R1を求めると、

　　R1＝$\frac{6Ω×6Ω}{6Ω+6Ω}$＝$\frac{36Ω}{12Ω}$ ＝ 3Ω 　　　

図2のように、3Ωと3Ωの直列となり、直並列回路の合成抵抗R2=3Ω＋3Ω＝6Ω

手順②図３の並列回路の合成抵抗を求める

　手順①を終えると、図3の並列回路となりました。合成抵抗R3を求めてと、

R3=$\frac{6Ω×3Ω}{6Ω+3Ω}$＝$\frac{18Ω}{9Ω}$ ＝ 2Ω

したがって、答えはロの2Ωです

２０１９年度　下期　問2

問の直径2.6㎜、長さ10ｍの銅導線と同じ抵抗値はどれかっていう問題です。

電線の抵抗Rは下記の計算式になります

R=$\frac{ρL}{A}$　　（ρ：抵抗率　、L：長さ　、A：断面積　）
断面積Aは、円の面積の為、半径×半径×πです。　A=$\frac{D}{2}$×$\frac{D}{2}$×π＝$\frac{D^2}{4}$×π（D:直径）
R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$＝$\frac{4ρL}{D^2 π}$（ρ：抵抗率　、L：長さ　、A：断面積　）

　ここで、銅導線と銅導線を比較しているので、ρ:抵抗値は同じとなるのでρは仮で１とすると、

　R=$\frac{4ρL}{D^2 π}$＝$\frac{4×1×L}{D^2 π}$＝$\frac{4L}{D^2 π}$となるので、この式に問の数値を代入してみましょう。　　

　　R=$\frac{4L}{D^2 π}$＝$\frac{4×10m}{2.6㎜×2.6㎜×π}$=1.88Ω　　抵抗値は1.88Ωです　　

　したがって、問題中のイロハニの中から抵抗値1.88Ωに近い数値を求めろってことです。　

　イを見てみると、R=$\frac{ρL}{A}$＝$\frac{1×10ｍ}{5.5㎜^2}$=1.82Ω (ρ：１，Ｌ：10m ，Ａ：5.5mm²)
　ロを見てみると、R=$\frac{ρL}{A}$＝$\frac{1×10ｍ}{8㎜^2}$=1.25Ω (ρ：１，Ｌ：10m ，Ａ：8mm²)
　ハを見てみると、R=$\frac{4L}{D^2 π}$= $\frac{4×20m}{1.6㎜×1.6㎜×π}$=9.95Ω (ρ:１,Ｌ:20m ,D:1.6mm)
　ニを見てみると、R=$\frac{4L}{D^2 π}$= $\frac{4×5m}{3.2㎜×3.2㎜×π}$ =0.62Ω (ρ:１,Ｌ:5m ,D:3.2mm)

したがって、1.88Ωに値が近い答えはイです

≪他の回答≫

イロハニすべてに式を代入すると面倒ですよね、そんな時にはここに注目してくだい

　問の断面積と長さに注目！！　

長さＬ：10ｍ
　断面積Ａ　：A=$\frac{D}{2}$×$\frac{D}{2}$×π =$\frac{2.6}{2}$×$\frac{2.6}{2}$×π＝5.3mm²

抵抗率は同じため、要はこれに近い値をみればいいわけです。

　イを見てみると、Ｌ：10m ，Ａ：5.5mm²
　ロを見てみると、Ｌ：10m ，Ａ：8mm²
　ハを見てみると、Ｌ：20m ，A=$\frac{D}{2}$×$\frac{D}{2}$×π =$\frac{1.6}{2}$×$\frac{1.6}{2}$×π＝2.0mm²　
　ニを見てみると、Ｌ：5m , A=$\frac{D}{2}$×$\frac{D}{2}$×π =$\frac{3.2}{2}$×$\frac{3.2}{2}$×π＝8.0mm²

値が近いイが答えだとわかりますね。

２０１９年度　下期　問3

熱量と電力量の関係は　≪3600kJ=1kW・h≫ があります

電力量を求めると、W＝P×t =500W×１.5ｈ＝750Wh　　（90分 / 60分 =1.5 h)

電力量は1時間あたりなので、秒に変換すると、1時間は3600秒となりますので

熱量と電力量の関係は　≪3600kJ=3600ｋＷ・ｓ＝1kW・h≫より、

熱量は、　Q＝W×t=750×3600＝2,700,000J＝2,700kJ　

したがって、答えは2,700kJのニです。

２０１９年度　下期　問4

電圧の波形に対して電流の波形が進んでいるのか、遅れているのかっていう問題ですね。

回路にコンデンサを使用していると電流は電圧よりも90°進む波形となります。

波形が進むっていわれてもわからないですよね。電圧の波形の最大値（プラス側）を基準にしたときに、電流の波形の最大値（プラス側）が左側にあれば進み、右側にあれば遅れとなります。

　イを見てみると、電流の波形の最大値（プラス側）が右側なので遅れ（リアクトル回路）
　ロを見てみると、電流の波形の最大値（プラス側）が同じなので（抵抗回路）
　ハを見てみると、電流の波形の最大値（プラス側）が右側なので遅れ（コンデンサ回路）
　ニを見てみると、電流の波形の最大値（プラス側）が右側なので遅れ

したがって、答えはハです

２０１９年度　下期　問5

　三相交流の問題ですね。回路はY（スター）回路となっています。

スター回路は、線間電圧Vℓ＝√3×相電圧Vp　、線電流Iℓ＝相電流Ip　の関係があります

相電圧Vｐ：抵抗両端の電圧（黄色枠部分）　　線間電圧Vℓ：線と線の間の電圧（赤枠部分）

まずは、相電圧Vpを求めましょう。Vp=$\frac{線間電圧Vℓ}{√3}$ ＝$\frac{210V}{√3}$＝121.3V

電流Iは、I= $\frac{相電圧 Vp}{インピーダンスZ}$＝$\frac{121.3V}{10Ω}$ ＝12.1A

したがって、答えは12.1Aのですロです。

参考：Δ回路について

　Δ回路の線間電圧と相電圧、線電流と相電流の関係性は、下記の通りです。

　Δ回路は、線間電圧Vℓ＝相電圧Vp　、線電流Iℓ＝√3相電流IP

２０１９年度　下期　問6

　中性線が無い状況なので、図を整理すると、下記図のようになります。

　　ただの直列回路なので、電流値を求めると、I＝$\frac{200V}{100Ω＋20Ω}$＝1.67A

　　a-b間の電圧Vabは、 Vab=I× 100Ω＝1.67A×100Ω＝167V

したがって、答えは167Vのハです

２０１９年度　下期　問7

　三相3線式の電圧降下の問題ですね。

これは公式があるので覚えましょう。（電験三種を受けるっていう方は基本から理解したほうがいいですが、電工の場合は公式を暗記して解きましょう）

　三相3線式の電圧降下（VｓーVr）＝√3 ×電流Ｉ×抵抗r　

　数値を代入すると、（VｓーVr）＝√3 ×電流Ｉ×抵抗r　＝√3×10Ａ×0.15Ω＝ 2.60Ｖ

　したがって、答えは2.6Ｖのロです

ちなみに、単相2線式、単相3線式の電圧降下の公式は、下記の通りです。

	電圧降下公式
単相2線式	2Ir
単相3線式	Ir
三相3線式	√3 Ir

２０１９年度　下期　問8

絶縁電線の許容電流についは表の通りです

表より、断面積5.5mm²の許容電流は49Ａなので、

電線1本あたりの許容電流は、　電線1本あたりの許容電流＝49A×0.70=34.3A

したがって、近い34Aとなり、答えはロです。

単線		より線
直径(mm)	許容電流（A)	断面積（mm²)	許容電流（A)
1.6	27	2	27
2.0	35	3.5	37
2,6	48	5.5	49
3.2	62	8	61

許容電流とは、絶縁電線やケーブルに流すことのできる最大電流のことです。つまり、この電流以上に電流を流すと電線が発熱し、電線が溶けたり、燃えてしまいます。

２０１９年度　下期　問9

分岐回路の過電流遮断器の取り付け箇所は、幹線の分岐点から３ｍ以下の箇所に過電流遮断器を設置しないといけないですが、次の条件により3m以上の位置に取り付けできます

下記の公式は覚えましょう

3ｍ以上～8ｍ以下：IW≧IB×0.35　（Iw：電線の許容電流、IB:幹線の過電流遮断器の定格電流）
８m以上：IW≧IB×0.55

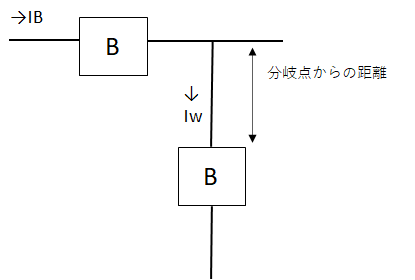
　低圧屋内幹線から分岐して7mの位置とあるので、分岐点から8ｍ以下なので電線の許容電流はIwは、

Iw≧IB×0.35=50A×0.35＝17.5A　　

したがって、答えは17.5Aのロです

２０１９年度　下期　問10

≪配線用遮断器の定格≫と≪コンセントの定格≫、≪電線の太さ≫の条件として、下記表を参照。

分岐回路	コンセント	電線の太さ
15A	15A以下	1.6㎜以上
20A 配線用遮断器	20A以下	1.6mm以上
20A ヒューズ	20A	2.0mm以上
30A	20～30A	2.6mm以上断面積5.5mm²以上
40A	30～40A	断面積8.0mm²以上
50A	40～50A	断面積14.0mm²以上