第二種電気工事士 (電工二種 ) 筆記試験の計算問題ですが、電気科出身じゃないので計算問題が不安、計算問題が苦手でどうすれば点数が取れるの?という方は多いのではないでしょうか。
電工二種の計算問題は毎年同じような問題が出題される為、解き方を覚えてしまえば簡単に20点取れます。合格点は60点なので1/3を稼げるので計算問題は合格するうえで重要なポイントです。
この記事では、2021年まで良く出題された問題を厳選し、同じ分野ごとに計算問題をまとめていますので全て読んで頂ければ計算問題がだいぶできるようになります。
それではどうぞ!!

直流回路編(問1)
問1では直流回路の合成抵抗や電流、電圧等を求める問題が多いです。
2020年度 下期 午前 問1

パッと見難しいそうですが、回路の末端(右側)から抵抗を合成していけば簡単に求められます。

上図のように、①→②の順に回路をまとめる
- ①:4Ωと4Ωの並列回路となっているので、合成抵抗は、$\frac{4×4}{4+4}$=2Ωとなります
- ②:2Ωと2Ωが直列となっているので4Ωとなります。次に、4Ωと4Ωの並列回路となっているので、2Ωとなります。
ここまで、回路をまとめると、一番右側の回路のような簡易な直列回路となります。
電流を求めるには、オームの法則により、
I=$\frac{V}{R}$=$\frac{16V}{2Ω+2Ω}$=4A
したがって、答えはハの4Aです
2019年度 上期 問1

1.スイッチ部分に注目し、抵抗を求める
2.開放部分のa-b間に注目し、抵抗を求める
3. 1,2より、回路を簡易化し、a-b間の電圧を求める
この問題は短絡・開放時に回路がどのようになるのかを問う問題ですね

1.スイッチ部分に注目し、抵抗を求める
スイッチ(S)を閉じたとき、図1の①部分に注目してもらうと短絡状態となっています。短絡すると、0Ωと50Ωに対してどっちに電流が流れるかとなると、抵抗が無い0Ωにすべて電流が流れますよね、したがって、①は0Ωとなります。
うーん、わかりにくいなと思う方は、0Ωと50Ωが並列回路だったときを考えてみてください。合成抵抗はどうなるでしょうか。
合成抵抗 = $\frac{(0Ω×50Ω)}{(0Ω+50Ω)}$= 0Ω
したがって、①部分は0Ωになります。
2.開放部分のa-b間に注目し、抵抗を求める
次に、図2の②に注目してください、a-b間は回路が開放しているので②に電流は流れないので0Ωとなります。a-b間はスイッチを開放している状態と思ってもらえるといいかもしれません。家の照明スイッチを切っていれば照明は点灯しませんよね?それって回路が開放されているため、電流が流れていないからです。
したがって、②部分は0Ωになります。
3. 1,2より、回路を簡易化し、a-b間の電圧を求める
手順①②を整理してみると、図3のように抵抗2つの直列回路となりとても簡単となります。
電流を求めてみましょう。 オームの法則より、電流I=$\frac{V}{R}$=$\frac{120}{(50+50)}$=1.2A
次に端子間abにかかる電圧Vabは、50Ωにかかる電圧のことなので、
Vab=IR=1.2A ×50Ω=60V
したがって、答えはニの60Vです
2018年度(下期) 問1
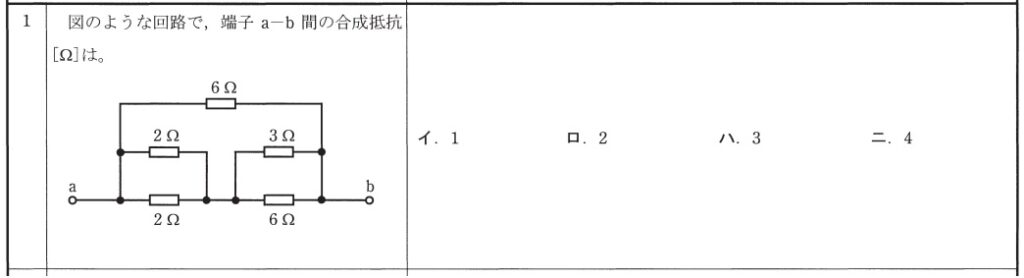
1 下の並列回路2か所の合成抵抗を求め、抵抗値を合計する
2 a-b間の合成抵抗を求める
1. 下の並列回路2か所の合成抵抗を求め、抵抗値を合計する

図1の赤色丸の2Ωと2Ω、水色丸の3 Ωと6Ω の各並列回路の合成抵抗を求める
- 赤色丸: R1= $\frac{2Ω×2Ω }{2Ω+2Ω }$= $\frac{4}{4}$=1Ω
- 水色丸: R2= $\frac{3Ω×6Ω }{3Ω+6Ω }$= $\frac{18}{9}$=2Ω
- 並列回路2か所を合成すると、図2のように直列回路となるので、合計するとR1+R2=1Ω+2Ω=3Ωと図3のようになります。
2. a-b間の合成抵抗Rabを求める
1.より、図3のような並列回路となりますので、 3 Ωと6Ωの並列回路の合成抵抗Rabは、
Rab=$\frac{3Ω×6Ω }{3Ω+6Ω }$= $\frac{18}{9}$=2Ω
したがって、答えはロです
2018年度(上期) 問1

1 スイッチSを閉じた際の並列回路の合成抵抗を求める
2 開放部分の抵抗について
3 電流を求める
4 a-b間の電圧Vabを求める
一見、ややこしいスイッチがあったり、回路が開放していたりとややこしく思えますが、手順通り解いてみましょう
1 スイッチSを閉じた際の並列回路の合成抵抗を求める

スイッチSを閉じた図は上記となります。赤丸部分の合成抵抗Rを求めるますが、下側は0Ωなので、0Ωになります。
計算すると、 R=$\frac{30Ω×0Ω}{30Ω+0Ω }$=$\frac{0}{30}$=0Ω
2 開放部分の抵抗について
a-b間は回路が開放しているので緑丸には、電流は流れないので0Ωとなります。a-b間はスイッチを開放している状態と思ってもらえるといいかもしれません。家の照明スイッチを切っていれば照明は点灯しませんよね?それって回路が開放されているため、電流が流れていないからです。
3 電流を求める

1,2をまとめると上記図のような直列回路となります。電流Iは、I =$\frac{V}{R}$=$\frac{100V}{30Ω+30Ω}$= $\frac{5}{3}$ A
4 a-b間の電圧Vabを求める
a-b間の電圧Vabは、電流×抵抗で求められるので、 電圧Vab= $\frac{5}{3}$ A ×30Ω= 50V となります。
したがって、答えはハです
2017年度(下期) 問1

1 電流を求める
2 回路のa-b間を短絡して、回路を上または下で分け電圧を求める
一見、見たことない回路で難しく感じますよね?ただ、計算の手順としてはオームの法則を知っていれば解くことができます。基本的には与えられた数値とオームの法則で解くことができるので特殊なことは特に何もしません。計算手順を解説します
1. 電流を求める
電流Iはオームの法則より、I=$\frac{V}{R}$なので、I=$\frac{100V+100A}{40Ω+60Ω}$=2A
2. 回路のa-b間を短絡して、回路を上または下で分け電圧を求める

上図のようにa-b間を短絡して回路わけてみると、上回路は図1、下回路は図2となります。
図1で電圧を求めてみると、1.より電流は2Aなので、40Ωにかかる電圧は、2A×40Ω=80Vとなります。
したがって、a-b間の電圧Vabは、Vab=100V-80V=20Vとなります。
したがって、答えはイです
念のため、図2でも同様に確認すると、60Ωにかかる電圧は2A×60Ω=120Vとなります。
したがって、a-b間の電圧は、100V-120V=-20Vとなります。マイナスとなっていますが、電流の向きが反対との意味となります。
電線の抵抗値(問2)
問2では、電線の抵抗値を求める問題が多く出題されます。出題パターンは少なく抵抗を求める計算式は覚えましょう。
電線の抵抗Rは下記の計算式になります
- R=$\frac{ρL}{A}$ (ρ:抵抗率 、L:長さ 、A:断面積 )
- 断面積とはここでいうと、円の面積の為、半径×半径×πです。整理すると、
A=$\frac{D}{2}$×$\frac{D}{2}$×π =$\frac{D^2}{4}$×π (D:直径) これを上記式に代入すると、 - R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$=$\frac{4ρL}{D^2 π}$(ρ:抵抗率 、L:長さ 、A:断面積 )
2020年度 下期 午前 問2

電線の抵抗Rは下記の計算式になります
- R=$\frac{ρL}{A}$ (ρ:抵抗率 、L:長さ 、A:断面積 )
- 断面積とはここでいうと、円の面積の為、半径×半径×πです。整理すると、 A=$\frac{D}{2}$×$\frac{D}{2}$×π =$\frac{D^2}{4}$×π (D:直径) これを上記式に代入すると、
- R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$=$\frac{4ρL}{D^2 π}$(ρ:抵抗率 、L:長さ 、A:断面積 )
上記抵抗の式ですが、抵抗A,Bの比較の為、長さL、直径D のみに注目してみとR=L/D^2となります
したがって、抵抗RA,RBに数値を代入すると、
- 抵抗RA=$\frac{L}{D^2}$=$\frac{20}{1.6^2}$=7.81
- 抵抗RB=$\frac{L}{D^2}$=$\frac{40}{3.2^2}$=3.91
抵抗RAは抵抗RBの何倍でしょうか。
抵抗RA/抵抗RB=$\frac{7.81}{3.91}$ =2
したがって、答えは2倍のイです
2019年度 下期 問2

問の直径2.6㎜、長さ10mの銅導線と同じ抵抗値はどれかっていう問題です。
電線の抵抗Rは下記の計算式になります
- R=$\frac{ρL}{A}$ (ρ:抵抗率 、L:長さ 、A:断面積 )
- 断面積Aは、円の面積の為、半径×半径×πです。 A=$\frac{D}{2}$×$\frac{D}{2}$×π=$\frac{D^2}{4}$×π(D:直径)
- R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$=$\frac{4ρL}{D^2 π}$(ρ:抵抗率 、L:長さ 、A:断面積 )
ここで、銅導線と銅導線を比較しているので、ρ:抵抗値は同じとなるのでρは仮で1とすると、
R=$\frac{4ρL}{D^2 π}$=$\frac{4×1×L}{D^2 π}$=$\frac{4L}{D^2 π}$となるので、この式に問の数値を代入してみましょう。
R=$\frac{4L}{D^2 π}$=$\frac{4×10m}{2.6㎜×2.6㎜×π}$=1.88Ω 抵抗値は1.88Ωです
したがって、問題中のイロハニの中から抵抗値1.88Ωに近い数値を求めろってことです。
- イを見てみると、R=$\frac{ρL}{A}$=$\frac{1×10m}{5.5㎜^2}$=1.82Ω (ρ:1,L:10m ,A:5.5mm2)
- ロを見てみると、R=$\frac{ρL}{A}$=$\frac{1×10m}{8㎜^2}$=1.25Ω (ρ:1,L:10m ,A:8mm2)
- ハを見てみると、R=$\frac{4L}{D^2 π}$= $\frac{4×20m}{1.6㎜×1.6㎜×π}$=9.95Ω (ρ:1,L:20m ,D:1.6mm)
- ニを見てみると、R=$\frac{4L}{D^2 π}$= $\frac{4×5m}{3.2㎜×3.2㎜×π}$ =0.62Ω (ρ:1,L:5m ,D:3.2mm)
したがって、1.88Ωに値が近い答えはイです
≪他の回答≫
イロハニすべてに式を代入すると面倒ですよね、そんな時にはここに注目してくだい
問の断面積と長さに注目!!
- 長さL:10m
- 断面積A :A=$\frac{D}{2}$×$\frac{D}{2}$×π =$\frac{2.6}{2}$×$\frac{2.6}{2}$×π=5.3mm2
抵抗率は同じため、要はこれに近い値をみればいいわけです。
- イを見てみると、L:10m ,A:5.5mm2
- ロを見てみると、L:10m ,A:8mm2
- ハを見てみると、L:20m ,A=$\frac{D}{2}$×$\frac{D}{2}$×π =$\frac{1.6}{2}$×$\frac{1.6}{2}$×π=2.0mm2
- ニを見てみると、L:5m , A=$\frac{D}{2}$×$\frac{D}{2}$×π =$\frac{3.2}{2}$×$\frac{3.2}{2}$×π=8.0mm2
値が近いイが答えだとわかりますね。
2019年度 上期 問2

この問題は許容電流を問う問題です。
許容電流とは、絶縁電線やケーブルに流すことのできる最大電流のことです。つまり、この電流以上に電流を流すと電線が発熱し、電線が溶けたり、燃えてしまいます。
電線の抵抗Rは下記の計算式になります
- R=$\frac{ρL}{A}$ (ρ:抵抗率 、L:長さ 、A:断面積 )
- 断面積とはここでいうと、円の面積の為、半径×半径×πです。整理すると、
A=$\frac{D}{2}$×$\frac{D}{2}$×π =$\frac{D^2}{4}$×π (D:直径) これを上記式に代入すると、 - R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$=$\frac{4ρL}{D^2 π}$(ρ:抵抗率 、L:長さ 、A:断面積 )
ロ、ハは上記の式により、正しいことがわかります
ニはDが大きくなると、抵抗が小さくなるので、許容電流が大きくなることがわかります
イは式にはないですが、温度上昇すると、放熱性が悪くなり、許容電流は小さくなります
したがって、答えはイです
2017年度(上期) 問3

電線の抵抗Rは下記の式によって、求められる
R=$\frac{ρL}{A}$ (ρ:抵抗率 、L:長さ 、A:断面積 )
※断面積Aは、円の面積の為、半径×半径×πです。 A=$\frac{D}{2}$×$\frac{D}{2}$×π=$\frac{D^2}{4}$×π(D:直径)
R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$=$\frac{4ρL}{D^2 π}$
電線の抵抗Rは下記の計算式となります。
- R=$\frac{ρL}{A}$ (ρ:抵抗率 、L:長さ 、A:断面積 )
- 断面積Aは、円の面積の為、半径×半径×πです。 A=$\frac{D}{2}$×$\frac{D}{2}$×π=$\frac{D^2}{4}$×π(D:直径)
- R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$=$\frac{4ρL}{D^2 π}$(ρ:抵抗率 、L:長さ 、A:断面積 )
上記抵抗の式ですが、抵抗A,Bの比較の為、長さL、直径D のみに注目してみとR=L/D^2となります
したがって、抵抗RA,RBに数値を代入すると、
- 抵抗RA=$\frac{L}{D^2}$=$\frac{20}{1.6^2}$=7.81
- 抵抗RB=$\frac{L}{D^2}$=$\frac{40}{3.2^2}$=3.91
抵抗RAは抵抗RBの何倍でしょうか。
抵抗RA/抵抗RB=$\frac{7.81}{3.91}$ =2
したがって、答えはイです。
電力量と熱量の関係 (問3)
問3では、電力量⇔熱量に変換できるのかを問われる問題が出題され、出題パターンは少ないです。
熱量と電力量の関係は ≪3600kJ=1kW・h≫ があります
2021年度(上期 午前) 問3

熱量と電力量の関係は ≪3600kJ=1kW・h≫ があります
電力を求めると、 P=I2×R=20A×20A×0.5Ω=200W
次に、1時間あたりの電力量を求めると、W=P×t =20W×1h=200Wh
電力量は1時間あたりなので、秒に変換すると、1時間は3600秒となりますので
熱量と電力量の関係は ≪3600kJ=3600kW・s=1kW・h≫より、
熱量は、 Q=W×t=200×3600=720000J=720kJ
したがって、答えは720kJのハです。
2019年度 上期 問3

この問題は、電力量(kW・h)を求める問題ですね
熱量と電力量の関係は ≪3600kJ=1kW・h≫ があります
水60㎏を20K上昇させる熱量は、水の比熱4.2kJ/(kg・K)により、
熱量=4.2kJ/(kg・K) ×60kg×20K =5040 kJ となります。
したがって、電力量は、5040kJ/3600 =1.4 kW・h 答えはハです
交流回路 (問4)
問4では、交流回路の消費電力、力率、電圧を求める問題が多く出題されます。
2021年度(上期 午後) 問4

抵抗、リアクタンス、全体に流れている電流値は問に記入されている為、求めやすいです。
力率cosθは、回路全体に流れる電流Iと抵抗に流れる電流IRによって求められます。
cosθ=$\frac{IR}{I}$=$\frac{6A}{10A}$ =0.6 ×100%=60%
したがって、答えはロです
2021年度(上期 午前) 問4

並列回路となっていますが、問題は回路の消費電力を問う問題です。つまり、抵抗で消費する電力を聞かれています。ラッキーなことに抵抗もリアクトルの両端には100Vなので、リアクトルは無視して大丈夫です。
抵抗に流れる電流Iは、 I=$\frac{100V}{16Ω}$=6.25 A
抵抗で消費する電力Pは、 P=電流I2×抵抗R=6.25A 2 ×16Ω=625W
したがって、答えはロです
2020年度 下期 午前 問4

力率は、$\frac{R}{Z}$×100%=$\frac{R}{\sqrt{R^2+X^2}}$×100%
したがって、答えはロです
これは、重要なので覚えるしかないですね
2019年度 上期 問4

まずは、インピーダンスZと電流Iを求めましょう
インピーダンスZ=$\sqrt{R^2+X^2}$=$\sqrt{8^2+6^2}$=$\sqrt{100}$=10Ω
電流I= $\frac{V}{Z}$=$\frac{100V}{10Ω}$=10A
抵抗8Ωの両端の電圧VRは、VR=電流I×抵抗R=10A×8Ω=80V
したがって、答えはニです
2018年度(上期) 問2

1 リアクタンスを求める
2 60Hzのときのリアクタンスを求める
3 60Hzのときの電流を求める
1 リアクタンスを求める
リアクタンスXは、電圧V、電流Iより、X=$\frac{電圧V}{電流I}$=$\frac{100V}{6A}$= $\frac{50}{3}$Ω となります。
2 60HzのときのリアクタンスX’を求める
リアクタンスXは、 X= ${2πfL}$ によって求められます。(f:周波数(Hz) 、 L:コイル(H) )
周波数を50Hz → 60Hzになると、 $\frac{60Hz}{50Hz}$=1.2倍になるので、X’= $\frac{50}{3}$Ω ×1.2 =20Ω となります。
3 60Hzのときの電流を求める
60Hzのときの電流Iは、電圧VとリアクタンスX’により求めらるので、電流Iは、
I= $\frac{電圧V}{リアクタンスX’}$ = $\frac{100V}{20Ω}$ = 5A
したがって、答えはロです
2017年度(上期) 問2

各電圧値により、力率を求める
1. 各電圧値により、力率を求める
電源電圧204V、抵抗に掛かる電圧180Vと問で与えられているので、力率cosθは、
cosθ= $\frac{VR}{V}$ = $\frac{180V}{204V}$=0.882 =88.2%となります。
したがって、答えはニです
三相回路 (問5)
問5では、三相回路の消費電力、電圧値等を求める問題が出題されますです。
Y(スター)回路とΔ(デルタ)回路は似ていてややこしいので、違いは区別できるようにしましょう。
【 Y(スター)回路 】
Y回路は、線間電圧E=√3×相電圧V 、線電流I=相電流I の関係があります
相電圧V:抵抗両端の電圧(黄色枠部分) 線間電圧E:線と線の間の電圧(赤枠部分)

【Δ(デルタ)回路】
Δ回路は、線間電圧E=相電圧V 、線電流I=√3×相電流I の関係があります
相電圧V:抵抗両端の電圧(赤枠部分) 線間電圧E:線と線の間の電圧(黄色部分)

2020年度 下期 午前 問5

三相誘導電動機の電力は、 P=√3VIcosθ (W)です
消費電力量はW=Pt(kW・h)なので、P=$\frac{W}{t}$に式を変換し、Pに上記式を代入すると、
P=√3VIcosθ=$\frac{W}{t}$ ×103 (W)
※103が出てきた理由は、kW→W へ変換したため 例)1kW=1000W
ここで、力率cosθを求めます
cosθ=$\frac{W}{√3VIt}$×103×100= $\frac{W}{√3VIt}$×105
したがって、答えはニです
2018年度(上期) 問5

1 相電圧を求める
2 線間電圧Eを求める
【ポイント】
Y回路は、線間電圧E=√3×相電圧V 、線電流I=相電流I の関係があります
相電圧V:抵抗両端の電圧(黄色枠部分) 線間電圧E:線と線の間の電圧(赤枠部分)

1 相電圧を求める
相電圧Vは、オームの法則より、相電流×インピーダンスZによって求められます。
相電圧V=相電流I×インピーダンスZ=20A×6Ω =120V
2 線間電圧を求める
線間電圧Eは、√3×相電圧Vの関係性があるので、
線間電圧E=√3×相電圧V =√3× 120V= 207.6V =208Vとなります。
したがって、答えはハです。
参考:Δ回路について
Δ回路の線間電圧と相電圧、線電流と相電流の関係性は、下記の通りです。
Δ回路は、線間電圧E=相電圧V 、線電流I=√3相電流IP
2017年度(下期) 問5

1 インピーダンスZを求める
2 相電流Iを求める
3 消費電力Pを求める
【ポイント】
Δ回路は、線間電圧E=相電圧V 、線電流I=√3×相電流I の関係があります
相電圧V:抵抗両端の電圧(赤枠部分) 線間電圧E:線と線の間の電圧(黄色部分)

三相電力の求め方は主に下記の3パターンあります
- 三相電力P=√3×線間電圧Vℓ×線間電流Iℓ×力率cosΘ (W)
- 三相電力P=3×相電圧Vp×相電流Ip×力率cosΘ (W)
- 三相電力P=3×相電流Ip2×抵抗 (W)
1 インピーダンスZを求める
1相当たりのインピーダンスZは、抵抗6Ωとリアクタンス8Ωの直列回路なので、インピーダンスZは、
Z=$\sqrt{R^2+X^2}$=$\sqrt{6^2 +8^2 }$=$\sqrt{100}$=10Ω
2 相電流をを求める
線間電圧E=相電圧Vなので、相電圧は200V、
相電流は、相電流I= $\frac{相電圧V}{インピーダンスZ}$= $\frac{200V}{10Ω}$=20A となります。
3 消費電力Pを求める
消費電力Pは何通りかで求めることができますが、力率を使用しない 3×相電流Ip2×抵抗 (W) を使って求めます。
消費電力P= 3×相電流I2×抵抗 =3× 20A2×6Ω= 7200W =7.2kWとなります。
したがって、答えはハです。
2017年度(上期) 問5

1 断線前のa-o間の電圧V(相電圧)を求める
2 断線後のa-o間の電圧Vを求める
【ポイント】
Y回路は、線間電圧E=√3×相電圧V 、線電流I=相電流I の関係があります
相電圧V:抵抗両端の電圧(黄色枠部分) 線間電圧E:線と線の間の電圧(赤枠部分)

1 断線前のa-o間の電圧V(相電圧)を求める

断線前のa-o間の電圧は相電圧Vなので、V=$\frac{線間電圧}{√3}$ =$\frac{200V}{√3}$=115.6=116V
2 断線後のa-o間の電圧Vを求める

断線後はa-o-b間には電圧200Vが掛かっています。
つまり、a-o間、o-b間は電圧が等しいので$\frac{200V}{2}$=100Vとなります。
したがって、答えはイです。
単相2線式回路(問6)
問6では、 単相2線式回路 の電線間の電圧、電圧降下を求める問題が多く出題されます。
2021年度(上期 午後) 問6

一見、難しい問題かと思いますが、右端から順に1つ1つ片づければ簡単です。
それでは、計算してみます
- c-c’間の抵抗は、抵抗負荷=$\frac{c-c’間の電圧Vc-c’}{c-c’間の電流Ic-c’}$=$\frac{100V}{5A}$=20Ω
- b-c-c’-b’間の抵抗は、Rb-c-c’-b’=0.1Ω+20Ω+0.1Ω=20.2Ω
- b-b’間の電圧は、Vb-b’=20.2Ω×5A=101V
- a-b間、b’-a’間の電流Ia-b=Ib’-a’は、Ia-b=Ib-c+Ib-b’=5A+5A=10A
それでは、a-b-b’-a間(a-a’間)の電圧を見ていきましょう
- a-b間の電圧は、Va-b=10A×0.05Ω=0.5V 、
- b’-a’間の電圧は Vb’-a’=10A×0.05Ω=0.5V
- a-b-b’-a’間(a-a’間)の電圧は、Va-b + Vb-b’ +Vb’-a’ = 0.5V+101V+0.5V=102V
したがって、答えは102Vのロです
2017年度(上期) 問6

1 配電線路10mの抵抗値を求める
2 電流を求める
3 配線における電圧降下を求める
1. 配電線路10mの抵抗値を求める

上記左図の赤丸内の配線10m分の抵抗値Rは、1000m当たり5Ωなので、
抵抗R= $\frac{10m}{1000m}$×5Ω= 0.05Ω となります。 上下の2本分あるので注意。(右図は抵抗値を記入)
2. 電流を求める
抵抗負荷1500Wにかかる電圧100Vは問で与えられているので、電力P=電圧V×電流Iの関係より、電流Iの式に変換すると、
電流I= $\frac{P}{V}$= $\frac{1500W}{100V}$=15A となります。
3. 配線における電圧降下vを求める
上記左図の赤丸の配線部分のみの電圧降下vを求めるので、1,2で求めた抵抗R、電流Iより
v=抵抗R×電流I+抵抗R×電流I=0.05Ω×15A + 0.05 Ω×15A =1.5V となります。
したがって、答えはハです
単相3線式回路(問7)
問7では、 単相3線式回路 の中性線(真ん中の線)が断線している場合や中性線 (真ん中の線) に電流が流れていない場合に電線の間の電圧、電力損失を求める問題が多く出題されます。
2021年度(上期 午後) 問7

中性線が断線してるので、ただの電圧200Vと100Ω、50Ωの直列回路となります。
電流値Iを求めると、I=$\frac{200V}{150Ω}$=1.33Aです
a-b間の電圧Vabとは、100Ωの両端の電圧のことなので、
Vab=電流I×100Ω=1.33A×100Ω=133V
したがって、答えはハです
2021年度(上期 午前) 問6

手順①:スイッチaのみを閉じる

- スイッチaのみとじると、上図のようになります。
- 電流I1を求めと、電力P=電圧V×電流Iより、 I1=$\frac{P}{V}$= $\frac{200W}{100V}$ =2A
手順②:スイッチa及びbを閉じる
- aとbの抵抗値を求めると、電力P=$\frac{電圧V^2}{抵抗R}$より、R=$\frac{V^2}{P}$=$\frac{100V^2}{200W}$=50Ω
- aとbの負荷に流れる電流は、I=$\frac{電圧V}{抵抗R}$=$\frac{100V}{50Ω}$=2A です。つまり、aとbでは同じ電流が流れている為、真ん中の線には電流がながれません。したがって、I2=0Aです。
したがって、答えは2のロです
2020年度 下期(午後) 問7

問題を見ると、右上・右下の抵抗負荷に20A流れていることがわかります。ということは、つまり中性線には電流が流れていないこととなり、下記の図になります

この回路の電線路の電力損失Pは、P=I2×r+I22×r=2I2×rとなるので、
P=2×I2×r=2×20A×20A×0.1=80(W)
したがって、答えはハです
2020年度 下期 午前 問7

図を見てもらうと、上の抵抗に15A流れ、下の抵抗にも15Aが流れていることがわかります
ということは、中性線には電流が流れていないことがわかります
この回路の電線路の電力損失Pは、P=2×I2×rとなるので、
P=2×I2×r=2×15A×15A×0.1=45 W
したがって、答えはイです
2018年度(上期) 問7

1 b点の電流10Aみると、aから10A流れて中性線には流れず下に10Aが流れていることがわかる
2 a-b間の電圧Vabを求める
1 中性線には電流が流れていないため、b点以下の配線を無視すると下記図のような簡易的な回路となるります。

2 a-b間の電圧Vab を求める
a-b間の電圧Vabは、Vab =電源電圧ー電圧降下分 (0.2Ωの電圧降下分)によって求められるので、
Vab =電源電圧ー電圧降下分 =104Vー0.2Ω×10A =102V となります。
したがって、答えはハです
絶縁電線の許容電流(問8)
問8では、 絶縁電線の許容電流を求める問題が出題されます。
2021年~2017年度の直近10回分の絶縁電線の許容電流 の問題では、下記表の『 直径1.6㎜、2.0㎜、断面積3.5 mm2、5.5mm2 』しか出ていないので最低この4つの場合の許容電流は覚えましょう。
許容電流とは、絶縁電線やケーブルに流すことのできる最大電流のことです。つまり、この電流以上に電流を流すと電線が発熱し、電線が溶けたり、燃えてしまいます。
| 単線 | より線 | ||
| 直径(mm) | 許容電流(A) | 断面積(mm2) | 許容電流(A) |
| 1.6 | 27 | 2 | 27 |
| 2.0 | 35 | 3.5 | 37 |
| 2,6 | 48 | 5.5 | 49 |
| 3.2 | 62 | 8 | 61 |
2021年度(上期 午前) 問8

絶縁電線の許容電流についは表の通りです
表より、断面積5.5mm2の許容電流は49Aなので、
電線1本あたりの許容電流は、 電線1本あたりの許容電流=49A×0.49=24A
したがって、答えはハです。
| 単線 | より線 | ||
| 直径(mm) | 許容電流(A) | 断面積(mm2) | 許容電流(A) |
| 1.6 | 27 | 2 | 27 |
| 2.0 | 35 | 3.5 | 37 |
| 2,6 | 48 | 5.5 | 49 |
2019年度 上期 問8

絶縁電線の許容電流についは表の通りです
表より、直径2.0mmの許容電流は35Aなので、
電線1本あたりの許容電流は、 電線1本あたりの許容電流=35A×0.56=19.6A
したがって、近い19Aとなり、答えはハです。
| 単線 | より線 | ||
| 直径(mm) | 許容電流(A) | 断面積(mm^2) | 許容電流(A) |
| 1.6 | 27 | 2 | 27 |
| 2.0 | 35 | 3.5 | 37 |
| 2,6 | 48 | 5.5 | 49 |
| 3.2 | 62 | 8 | 61 |
幹線の許容電流 (問9)
問9では、 幹線の許容電流又は次項目の電流遮断器の取り付け箇所の条件 を求める問題が出題されます。
幹線の許容電流Iw を求めるには、下記表を覚えないといけないので必ず覚えましょう。

※IM:電動機の定格電流 、 その他負荷の定格容量IH
条件①は、電動機の定格電流IMよりその他の定格容量IHが大きい場合。
許容電流Iw=IM + IH
条件②は 、電動機の定格電流IMがその他の定格容量IHが大きい場合。
さらに、 電動機の定格電流IM が50A以上の場合、 許容電流Iw=1.25IM + IH
電動機の定格電流IM が50A以下の場合、 許容電流Iw= 1.1IM + IH
2020年度 下期(午後) 問9

許容電流Iwを求める問題ですね。Iwを求めるには下の表を使って求めます

※IM:電動機の定格電流 、 その他負荷の定格容量IH
電動機5台の定格電流の合計は需要率が80%なので定格電流IMは、
IM=12A×5台×0.8=48A ※その他負荷は無いのでIH=0
表より、条件②が該当し、IM≦50A以下なので、許容電流Iwは、1.25IMとなることがわかります。
したがって、Iw=1.25×48A=60A
答えは60Aのロです
2020年度 下期 午前 問9

電線の許容電流Iwを求める問題です
条件としては下記の通りです※IM:電動機の定格電流 、 その他負荷の定格容量IH
| 条件① | IM ≦IH | Iw≧IM+IH | |
| 条件② | IM >IH | IM≦50A | Iw≧1.25IM+IH |
| IM>50A | Iw≧1.1IM+IH | ||
電動機の定格電流はIM=30A+30A+20A=80A
その他負荷の定格容量はIH=15A
今回は、条件②IM>IHのIM>50Aに該当します
許容電流Iwは、Iw=1.1IM+IH=1.1×80+15=103A
したがって、答えはロの103Aです
電流遮断器の取り付け箇所の条件 (問9)
問9では、 幹線の許容電流又は次項目の電流遮断器の取り付け箇所の条件 を求める問題が出題されます。
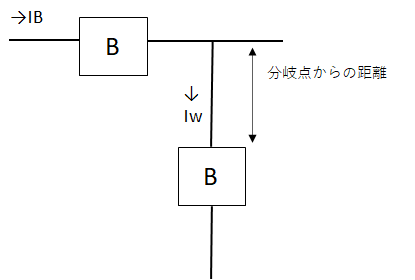
分岐回路の過電流遮断器の取り付け箇所の条件は、下記3通りです。
- 幹線の分岐点から3m以下の箇所に過電流遮断器を設置しないといけないですが、
次の条件により3m以上の位置に取り付けできます - 3m以上~8m以下:IW≧IB×0.35 (Iw:電線の許容電流、IB:幹線の過電流遮断器の定格電流)
- 8m以上:IW≧IB×0.55
2021年度(上期 午後) 問9

分岐回路の過電流遮断器の取り付け箇所の条件は、下記3通りです。
- 幹線の分岐点から3m以下の箇所に過電流遮断器を設置しないといけないですが、
次の条件により3m以上の位置に取り付けできます - 3m以上~8m以下:IW≧IB×0.35 (Iw:電線の許容電流、IB:幹線の過電流遮断器の定格電流)
- 8m以上:IW≧IB×0.55

イ、ロは、幹線の分岐点からL=3m以下なので適切
ハは、L=10mなので、8m以上:IW≧IB×0.55の条件となります。
幹線の過電流遮断器の定格電流IBの55%以上でなければいけません。
つまり、IB=100なので、許容電流Iw=55A以上となります。問では42Aなので不適切
ニは、L=15mなので、8m以上:IW≧IB×0.55の条件となります。
幹線の過電流遮断器の定格電流IBの55%以上でなければいけません。
つまり、IB=100なので、許容電流Iw=55A以上となります。問では61Aなので適切
したがって、答えはハです
2017年度(下期) 問10

【分岐回路の過電流遮断器の取り付け箇所の条件】は、下記3通りです。
- 幹線の分岐点から3m以下の箇所に過電流遮断器を設置しないといけないですが、次の2,3の条件により3m以上の位置に取り付けできます
- 3m以上~8m以下:IW≧IB×0.35 (Iw:電線の許容電流、IB:幹線の過電流遮断器の定格電流)
- 8m以上:IW≧IB×0.55

VVRケーブル太さ5.5mm2 の許容電流IWは34A、過電流継電器の定格電流IBは100Aと与えられています。
$\frac{ VVRケーブル太さ5.5mm^2の許容電流 IW }{ 過電流継電器の定格電流IB }$=$\frac{34A}{100A}$=0.34 となります。
過電流継電器の取付条件を見てみると、0.35以下の0.34なので、条件1に当てはまるので3m以下です。
したがって、答えはイです
配線用遮断器の定格・コンセントの定格・電線の太さ≫の組合せ条件(問10)
問10は、計算問題ではないですが、毎年必ず出題される問題なので下記表を覚えれば必ず解答できるので覚えましょう。
≪配線用遮断器の定格≫と≪コンセントの定格≫、≪電線の太さ≫の条件
| 分岐回路 | コンセント | 電線の太さ |
| 15A | 15A以下 | 1.6㎜以上 |
| 20A 配線用遮断器 | 20A以下 | 1.6mm以上 |
| 20A ヒューズ | 20A | 2.0mm以上 |
| 30A | 20~30A |
2.6mm以上 断面積5.5mm2以上 |
| 40A | 30~40A | 断面積8.0mm2以上 |
| 50A | 40~50A | 断面積14.0mm2以上 |
2021年度(上期 午後) 問10

≪配線用遮断器の定格≫と≪コンセントの定格≫、≪電線の太さ≫の条件として、
下記表を参照
| 分岐回路 | コンセント | 電線の太さ |
| 15A | 15A以下 | 1.6㎜以上 |
| 20A 配線用遮断器 | 20A以下 | 1.6mm以上 |
| 20A ヒューズ | 20A | 2.0mm以上 |
| 30A | 20~30A |
2.6mm以上 断面積5.5mm2以上 |
| 40A | 30~40A | 断面積8.0mm2以上 |
| 50A | 40~50A | 断面積14.0mm2以上 |
それぞれ条件を見てみると、
- イは分岐回路20Aに対して、電線の太さ1.6mm、定格電流15Aコンセントなので、適切
- ロは分岐回路30Aに対して、電線の太さ2.0 mmなので、不適切
- ハは分岐回路20Aに対して、電線の太さ2.0mm、定格電流20Aコンセントなので適切
- ニは分岐回路40Aに対して、電線の太さ断面積8.0mm2なので適切
したがって、答えはロです
2019年度 下期 問10

≪配線用遮断器の定格≫と≪コンセントの定格≫、≪電線の太さ≫の条件として、下記表を参照。
| 分岐回路 | コンセント | 電線の太さ |
| 15A | 15A以下 | 1.6㎜以上 |
| 20A 配線用遮断器 | 20A以下 | 1.6mm以上 |
| 20A ヒューズ | 20A | 2.0mm以上 |
| 30A | 20~30A |
2.6mm以上 断面積5.5mm2以上 |
| 40A | 30~40A | 断面積8.0mm2以上 |
| 50A | 40~50A | 断面積14.0mm2以上 |
分岐回路30Aの条件は、≪コンセントは20~30A≫、≪電線の太さ2.6㎜以上、断面積5.5mm2以上≫
- イは、電線の太さ 断面積5.5mm2なので適切だと思いますが、コンセントにアンペア数が書いていません、つまり、定格電流15Aなので、不適切
- ロは、電線の太さ 断面積3.5 mm2なので不適切
- ハは、電線の直径2.0mmなので不適切
- ニは電線の太さ 断面積5.5mm2、定格電流20Aコンセントなので適切
したがって、答えはニです
※コンセントにアンペア数が書いていないと、定格電流15Aとなります。
2018年度(上期) 問10

≪配線用遮断器の定格≫と≪コンセントの定格≫、≪電線の太さ≫の条件として、
下記表を参照
| 分岐回路 | コンセント | 電線の太さ |
| 15A | 15A以下 | 1.6㎜以上 |
| 20A 配線用遮断器 | 20A以下 | 1.6mm以上 |
| 20A ヒューズ | 20A | 2.0mm以上 |
| 30A | 20~30A |
2.6mm以上 断面積5.5mm2以上 |
| 40A | 30~40A | 断面積8.0mm2以上 |
| 50A | 40~50A | 断面積14.0mm2以上 |
それぞれ条件を見てみると、
- イは分岐回路20Aに対して、定格電流15Aコンセントなので適切
- ロは分岐回路20Aに対して、定格電流20Aコンセントなので適切
- ハは分岐回路30Aに対して、定格電流30Aコンセントなので適切
- ニは分岐回路30Aに対して、定格電流15Aコンセントなので不適切
したがって、答えはニです
以上、お疲れさまでした。
「出典:筆記試験 第ニ種電気工事士 :一般財団法人電気技術者試験センター 試験の問題と解答 | ECEE 一般財団法人電気技術者試験センター (shiken.or.jp)」
そのほかの問題については、下記リンクをご覧ください。


