【計算苦手な方】第二種電気工事士　2018年度（上期）筆記試験　問１～１０　計算問題　過去問解説

　第二種電気工事士　 2018年度（上期）筆記試験の問1～10について、解説していきます

計算問題は毎年似たような問題が出てくるため、点数を取りやすいです。今回の問題も過去問と変わらない問題ばかりです。ぜひ、最初の10問を完璧に解き20点を確保しましょう。

それではどうぞ！！

2018年度（上期）　問１
2018年度（上期）　問2
2018年度（上期）　問3
2018年度（上期）　問4
2018年度（上期）　問5
2018年度（上期）　問6
2018年度（上期）　問7
2018年度（上期）　問8
2018年度（上期）　問9
2018年度（上期）　問10

2018年度（上期）　問１

解き方

１　スイッチSを閉じた際の並列回路の合成抵抗を求める

２　開放部分の抵抗について

３　電流を求める

４　a-b間の電圧Vabを求める

　一見、ややこしいスイッチがあったり、回路が開放していたりとややこしく思えますが、手順通り解いてみましょう

１　スイッチSを閉じた際の並列回路の合成抵抗を求める

スイッチSを閉じた図は上記となります。赤丸部分の合成抵抗Rを求めるますが、下側は0Ωなので、０Ωになります。

計算すると、 R=$\frac{30Ω×0Ω}{30Ω+0Ω }$＝$\frac{0}{30}$=0Ω

２　開放部分の抵抗について

a-b間は回路が開放しているので緑丸には、電流は流れないので0Ωとなります。a-b間はスイッチを開放している状態と思ってもらえるといいかもしれません。家の照明スイッチを切っていれば照明は点灯しませんよね？それって回路が開放されているため、電流が流れていないからです。

３　電流を求める

１，２をまとめると上記図のような直列回路となります。電流Iは、I =$\frac{V}{R}$＝$\frac{100V}{30Ω+30Ω}$= $\frac{5}{3}$ A

４　a-b間の電圧Vabを求める

　 a-b間の電圧Vabは、電流×抵抗で求められるので、電圧Vab= $\frac{5}{3}$ A ×30Ω= 50V　となります。

したがって、答えはハです

2018年度（上期）　問2

解き方

１　リアクタンスを求める

２　60Hzのときのリアクタンスを求める

３　60Hzのときの電流を求める

１　リアクタンスを求める

リアクタンスXは、電圧V、電流Iより、X=$\frac{電圧V}{電流I}$＝$\frac{100V}{6A}$= $\frac{50}{3}$Ω　となります。

２　 60HzのときのリアクタンスX’を求める

　リアクタンスXは、 X= ${2πfL}$ によって求められます。（ｆ：周波数(Hz)　、　Ｌ：コイル(H) )

周波数を50Hz　→　60Hzになると、 $\frac{60Hz}{50Hz}$=1.2倍になるので、X’= $\frac{50}{3}$Ω ×1.2 =20Ω となります。

３　60Hzのときの電流を求める

　 60Hzのときの電流Iは、電圧VとリアクタンスX’により求めらるので、電流Iは、

I= $\frac{電圧V}{リアクタンスX’}$ = $\frac{100V}{20Ω}$ = 5A

したがって、答えはロです

2018年度（上期）　問3

解き方

電線の抵抗Rは下記の式によって、求められる

　R=$\frac{ρL}{A}$　　（ρ：抵抗率　、L：長さ　、A：断面積　）

　※断面積Aは、円の面積の為、半径×半径×πです。　A=$\frac{D}{2}$×$\frac{D}{2}$×π＝$\frac{D^2}{4}$×π（D:直径）

　R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$＝$\frac{4ρL}{D^2 π}$

電線の抵抗Rは下記の計算式となります。

R=$\frac{ρL}{A}$　　（ρ：抵抗率　、L：長さ　、A：断面積　）
断面積Aは、円の面積の為、半径×半径×πです。　A=$\frac{D}{2}$×$\frac{D}{2}$×π＝$\frac{D^2}{4}$×π（D:直径）
R=$\frac{ρL}{A}$=$ \frac{ρL}{(\frac{D^2}{\ \ 4\ \ }×π)}$＝$\frac{4ρL}{D^2 π}$（ρ：抵抗率　、L：長さ　、A：断面積　）

許容電流Iは、 I=$\frac{V}{R}$ですが、抵抗Rに上記式を代入すると、下記の計算式となります

I＝ $ \frac{V}{R}$ =$\frac{V×D^2 π}{4ρL}$

ロとハと二は上記の計算式で見てみると、

ロ：許容電流I （$\frac{V×D^2 π}{4ρL}$は、Dが大きくなると許容電流Iは大きくなるので正解です。
ハ：抵抗R（$\frac{4ρL}{D^2 π}$）は、Lに比例しているので正解です。
二：抵抗R（$\frac{4ρL}{D^2 π}$）は、D²に反比例しているので正解です。

イですが、式に無いですが、温度が上がると抵抗は大きくなる特徴があるので、許容電流は小さくなるので誤りです。

したがって、答えはイです。

2018年度（上期）　問4

解き方

１　電力量Wを求める

２　熱量Qを求める

≪ポイント≫

電力量Wと熱量Qはそれぞれ下記の計算式となります

　電力量W：W=P×t (kW・h) 　【P:消費電力 (kW)、t:時間(h)】

　熱量Q：Q= c×m×T(kJ)　【c:比熱 (kJ/(kg・K) )、m:質量(kg)、T:温度変化(K)】

　熱量Qと電力量Wの関係性　≪3600kJ=1kW・h≫ ※ Q=3600×W W=Q / 3600によってそれぞれ求められる

　電力量Wは、電力量W=P×t より、W=I²×R×t = 15A² ×0.2Ω×1h=45 W･h=0.045kW ･h となります　（消費電力P= I²×R)

　熱量Qと電力量Wの関係性　≪3600kJ=1kW・h≫ より、熱量Q=3600×Wによって求められるので、電力量をを代入すると、

　熱量Q=3600×W＝3600× 0.045kWh=162kJ となります。

したがって、答えはニです

2018年度（上期）　問5

解き方

1　相電圧を求める

2　線間電圧Eを求める

【ポイント】

　Y回路は、線間電圧E＝√3×相電圧V　、線電流I＝相電流I　の関係があります

相電圧V：抵抗両端の電圧（黄色枠部分）　　線間電圧E：線と線の間の電圧（赤枠部分）

１　相電圧を求める

　相電圧Vは、オームの法則より、相電流×インピーダンスZによって求められます。

　相電圧V=相電流I×インピーダンスZ=20A×6Ω =120V

２　線間電圧を求める

　線間電圧Eは、√3×相電圧Vの関係性があるので、

　線間電圧E=√3×相電圧V =√3× 120V= 207.6V =208Vとなります。

したがって、答えはハです。

参考：Δ回路について

　Δ回路の線間電圧と相電圧、線電流と相電流の関係性は、下記の通りです。

　Δ回路は、線間電圧E＝相電圧V　、線電流I＝√3相電流IP

2018年度（上期）　問6

解き方

1 配電線路16mの抵抗値を求める

2　電流を求める

3　配線における電圧降下を求める

1. 配電線路16mの抵抗値を求める　　

　　上記左図の赤丸内の配線16m分の抵抗値Rは、1000m当たり3.2Ωなので、

　　抵抗R= $\frac{16m}{1000ｍ}$×3.2Ω= 0.0512Ω　となります。　上下の2本分あるので注意。（右図は抵抗値を記入）

2. 電流を求める

　　抵抗負荷2000Wにかかる電圧100Vは問で与えられているので、電力P=電圧V×電流Iの関係より、電流Iの式に変換すると、

　　電流I= $\frac{P}{V}$= $\frac{2000W}{100V}$=20A　となります。

3.　配線における電圧降下vを求める

　上記左図の赤丸の配線部分のみの電圧降下vを求めるので、1,2で求めた抵抗R、電流Iより

　v=抵抗R×電流I＋抵抗R×電流I＝0.0512Ω×20A + 0.0512 Ω×20A =2.048V となります。

したがって、答えはロです

2018年度（上期）　問7

解き方

１　b点の電流10Aみると、aから10A流れて中性線には流れず下に10Aが流れていることがわかる

２　a-b間の電圧Vabを求める

1　中性線には電流が流れていないため、b点以下の配線を無視すると下記図のような簡易的な回路となるります。

２　 a-b間の電圧Vab を求める

　a-b間の電圧Vabは、Vab =電源電圧ー電圧降下分（0.2Ωの電圧降下分）によって求められるので、

　Vab =電源電圧ー電圧降下分＝104Vー0.2Ω×10A =102V となります。

　したがって、答えはハです

2018年度（上期）　問8

絶縁電線の許容電流についは表の通りです

表より、直径2.0mmの許容電流は３5Ａなので、

電線1本あたりの許容電流は、　電線1本あたりの許容電流＝35A×0.63=22A

したがって、答えはロです。

単線		より線
直径(mm)	許容電流（A)	断面積（mm²)	許容電流（A)
1.6	27	2	27
2.0	35	3.5	37
2,6	48	5.5	49
3.2	62	8	61

許容電流とは、絶縁電線やケーブルに流すことのできる最大電流のことです。つまり、この電流以上に電流を流すと電線が発熱し、電線が溶けたり、燃えてしまいます。

2018年度（上期）　問9

分岐回路の過電流遮断器の取り付け箇所の条件は、下記3通りです。

幹線の分岐点から３ｍ以下の箇所に過電流遮断器を設置しないといけないですが、次の2,3の条件により3m以上の位置に取り付けできます
3ｍ以上～8ｍ以下：IW≧IB×0.35　（Iw：電線の許容電流、IB:幹線の過電流遮断器の定格電流）
８m以上：IW≧IB×0.55

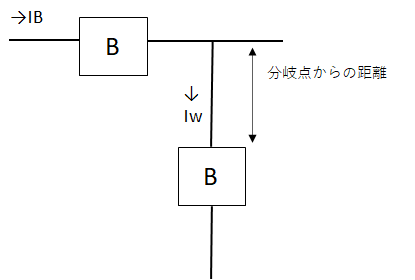
6mの位置にの過電流遮断器を取りtけるので、3ｍ以上～8ｍ以下：IW≧IB×0.35に該当します。

許容電流IW＝IB×0.35=100A×0.35＝35A

したがって、答えはロです

2018年度（上期）　問10

≪配線用遮断器の定格≫と≪コンセントの定格≫、≪電線の太さ≫の条件として、

下記表を参照

分岐回路	コンセント	電線の太さ
15A	15A以下	1.6㎜以上
20A 配線用遮断器	20A以下	1.6mm以上
20A ヒューズ	20A	2.0mm以上
30A	20～30A	2.6mm以上断面積5.5mm²以上
40A	30～40A	断面積8.0mm²以上
50A	40～50A	断面積14.0mm²以上