【計算苦手な方】第1種電気工事士　2018年度追加 筆記試験　問1～11　過去問解説

　第1種電気工事士　2018年度追加 筆記試験の問1～11について、解説していきます

計算問題は毎年似たような問題が出てくるため、点数を取りやすいです。今回の問題も過去問と変わらない問題ばかりです。

それではどうぞ！！

2018年度追加　問１

問は導体に電磁力F=LIBが発生するが、電磁力の方向を知るために用いられる法則を聞かれています。上記の法則をみてみると、フレミングの左手の法則だということがわかります。

したがって、答えはハです

2018年度追加　問2

1 直列・並列負荷に掛かる電圧を求める

≪回路の電圧について電源電圧は104V≫

直列の8Ωにかかる電圧は64Vということは、

並列回路(R1とR２)にかかる電圧は残りの40V（＝104V-64V）となります。

2　電流値を求める

直列の8Ωにかかる電圧は64Vということは、電流値I=$\frac{V}{R}$＝$\frac{64V}{8Ω}$＝8A

3　抵抗R1を求める

　抵抗R1、R2 の並列部分には40V。R2に流れる電流は6Aの為、R1に流れる電流は、８A-６A＝2Aとなります。

抵抗R1にかかる電圧と電流値がわかったので、抵抗R1=$\frac{40V}{2A}$ = 20Ω

したがって、答えはニです

2018年度追加　問3

１．インピーダンスZを求める

　インピーダンスZ=$\frac{V}{I}$ =$\frac{100V}{20A}$ = 5Ω

2．抵抗値を求める

　R= $\frac{VR}{I}$ =$\frac{80V}{20A}$= 4Ω

３．リアクタンスXを求める

　インピーダンス$\sqrt{R^2+X^2}$より、リアクタンスXは、X= $\sqrt{Z^2-R^2}$によって求められます。

リアクタンスX= $\sqrt{Z^2-R^2}$＝$\sqrt{5^2-4^2}$＝$\sqrt{9}$ = 3Ω

したがって、答えはロです。

2018年度追加　問4

１．各負荷に流れている電流値をI_R、I_L、I_{Cを求める}

　各負荷には電圧100Vが掛かっているので簡単に求められます

• 抵抗Rに流れる電流I_R＝ $\frac{100V}{5Ω}$ =20A
• インダクタンスLに流れる電流I_L =$\frac{100V}{10Ω}$ =10A
• コンデンサに流れる電流I_C =$\frac{120V}{10Ω}$ =10A

２．電流値Iを求める

　電流値I=$\sqrt{（IR^2+(IL-IC)^2)}$ より、I=$\sqrt{（20^2+(10-10)^2)}$=$\sqrt{400}$＝20A

したがって、答えはハです

2018年度追加　問5

1 リアクタンスのΔ回路をY回路へ変換する

Δ回路をY回路へ変換するには図1、２のように≪負荷の積 / 和≫で求めることができます。

例えば、Δ回路のR1とR2によって、Y回路のR12を求められる　　　　　　　　　　　　　　　　　　　　　　　　　　　　　R12= $\frac{R1×R2}{R1+R2+R3}$

同様にR23=$\frac{R2×R3}{R1+R2+R3}$ 、R31= $\frac{R3×R1}{R1+R2+R3}$のように求められる。

ただ、複数の文字を使っての数式だとわかりにくい部分があるので、Rのみで表すと、　　　　　　　　　R12=$\frac{R1×R2}{R1+R2+R3}$＝$\frac{R^2}{3R}$ = $\frac{R}{3}$ と、Δ回路 →Y回路へ変換すると1/ 3倍となります。

これをもとにリアクタンスをΔ回路からY回路へ変換すると、$\frac{9Ω}{3}$= 3Ωとなります。

下記の図はリアクタンスをΔ回路からY回路へ変換した図です。

2 インピーダンスZを求める

1相あたりのインピーダンスZ= $\sqrt{R^2+X^2}$より、Z= $\sqrt{R^2+X^2}$＝$\sqrt{4^2+3^2}$ =$\sqrt{25}$ =5 Ω

3 線電流を求める

　Y回路は線間電圧V＝√3×相電圧V　、線電流I＝相電流Iの関係があるのでこれを基に下記を求める

1. 相電圧を求める：相電圧＝$\frac{線間電圧V}{√3}$
2. 相電流を求める：相電流＝$\frac{相電圧}{インピーダンスZ}$ ＝$\frac{V}{√3×Z}$
3. 線電流を求める：線電流＝相電流なので、$\frac{V}{√3×Z}$=$\frac{V}{√3×5}$

したがって、答えはロです。

2018年度追加　問6

配電線路の電圧降下ｖは、v=『I（Rcosθ＋Xsinθ）+ I（Rcosθ＋Xsinθ）』によって求められます。

電流I：10A　、　R：0.4Ω　、　X：0.3Ω　、　力率0.8よりcosθ：0.8　、　　　　　　　　　　　　　　　　　　　　　　　sinθは、1=$\sqrt{cos^2θ1+sin^2θ1}$より、sinθ1=$\sqrt{1-cos^2θ1}$= $\sqrt{1-0.8^2}$=$\sqrt{0.36}$＝0.6 です。

電圧降下v=I（Rcosθ＋Xsinθ）+ I（Rcosθ＋Xsinθ）=２I（Rcosθ＋Xsinθ）に上記値を代入すると、

v= 2 I（Rcosθ＋Xsinθ）＝2×10A( 0.4Ω×0.8＋0.3Ω×0.6)=20×（0.5）＝10V

電源電圧Vsを求める

電源電圧Vs =電圧降下v + 負荷にかかる電圧＝10V + 200V = 210V

したがって、答えはロです

2018年度追加　問7

1　電流値を求める

三相負荷Pの公式は、P=√3VIcosθより、電流Iの形に変換すると、I= $\frac{P}{√3Vcosθ}$となります。

ここで、問の数値を代入したくなりますが、ちょっと待ってください。計算が複雑になってしまうので、次の電力損失まで数値を代入しないようにしましょう。

2　三相3線式の電力損失P_L=3I²rを求める

三相3線式の電力損失P_Lの公式は、P_L=3I²rです。

上記1より、電流IはI=$\frac{P}{√3Vcosθ}$です。これをP_L=3I²rに代入すると、

P_L=3I²r＝3×（$\frac{P}{√3Vcosθ}$)² ×r = 3 × $\frac{P^2}{3V^2cos^2θ}$×r = $\frac{P^2r}{V^2cos^2θ} $となり、ルート√の計算をしなくてもよくなり、計算も簡単にできるようになります。この式に数値を代入すると、

P_L=$\frac{P^2r}{V^2cos^2θ} $=$\frac{8000W^2×0.1Ω}{200V^2×0.8^2} $ = 250【A】　(P=8,000W、r=0.1Ω、V=200V、cosθ=0.8）

　したがって、答えはハです

2018年度追加　問8

一次側と二次側とは、図のようになります。一次側は電圧6000Vで高圧である為、二次側を変圧器によってコンセントで使用できる電圧（100 / 200V )に変圧します。

一次側の電力と、二次側の電力は同じとなりますので、まずは、情報がある二次側の電力を求めます。

１　二次側の抵抗値R1、R2を求める　

　抵抗R1は、R1=$\frac{V}{I}$ より、R1 = $\frac{V}{I}$= $\frac{100V}{40A}$ = 2.5Ω

　抵抗R2は、R2=$\frac{V}{I}$より、R2 = $\frac{V}{I}$= $\frac{100V}{20A}$= 5Ω

２　二次側の電力を求める

　抵抗R1での消費電力P₂₁は、P₂₁ = I² ×R1 = 40²×2.5Ω = 4000W

　抵抗R2での消費電力P₂₂は、P₂₂= I² ×R2 = 20²×5Ω = 2000W

二次側の合計電力は、P₂＝P₂₁ + P₂₂ =4000W + 2000W = 6000W

３　一次側の電流を求める

二次側の電力P₂と一次側の電力P₁は等しいので、P₁＝P₂＝6000W　です。

電流I1は、I1= $\frac{P1}{V}$ =$\frac{6000W}{6000V}$=1A

したがって、答えはイです。

≪別解：二次側の電力の求め方≫

二次側の抵抗値を求めなくても、P₂₁ 、 P₂₂は、電流×電圧で求めらるので、

P₂₁＝100V × 40A = 4000W 、 P₂₂＝100V × 20A = 2000W となり、

P₂＝P₂₁ + P₂₂ =4000W + 2000W = 6000W　となります。

計算に慣れてもらうために抵抗を求めて解説しました。面倒だと思う方はいきなり二次側の電力から求めてください

2018年度追加　問9

力率改善に必要なコンデンサの定格容量Qcを求める

力率を0.8 → 0.93 に改善する為に必要なコンデンサの定格容量Qcを求める公式は、

Qc＝P(tanθ1 – tanθ2) 　　※（tanθ =$\frac{sinθ}{cosθ}$ ）です。

この式に 各数値（P＝80kW、cosθ1=0.8、sinθ1=0.6、tanθ2=0.38）を代入すると、　

※sinθ1は、1=$\sqrt{cos^2θ1+sin^2θ1}$より、sinθ1=$\sqrt{1-cos^2θ1}$= $\sqrt{1-0.8^2}$=$\sqrt{0.36}$＝0.6

Qc＝P(tanθ1 – tanθ2) ＝P($\frac{sinθ1}{cosθ1}$ – tanθ2) ＝80($\frac{0.6}{0.8}$ – 0.38) ＝29.6【kvar】

したがって、答えはロです

≪参考：無効電力Q1、無効電力Q2を求めてみます≫

1　コンデンサ接続前の無効電力Q1【kvar】を求める

　皮相電力S1は問より100KVA、消費電力Pは80kWと与えられているので、　　　　　　　　　　　　　　　　　　　　　　　　　無効電力Q1は、Q1＝$\sqrt{S1^2-P^2}$=$\sqrt{100^2-80^2}$=60【kvar】

2　コンデンサ接続後の無効電力Q2【kvar】を求める

　皮相電力S2はP=Scosθより、コンデンサ接続後の力率0.93、消費電力80kWを代入すると、

S2=$\frac{P}{cosθ2}$=$\frac{80kW}{0.93}$=86【kVA】

無効電力Q2は、Q2＝$\sqrt{S2^2-P^2}$=$\sqrt{86^2-80^2}$ =31.6【kvar】

2018年度追加　問10

問をみると、②はR相＝V、S相＝Uが入れ替わっているので、逆方向に回転します

③は結線がR相＝V、S相＝W、T相＝Uと120°づつ入れ替えているので同じ方向に回転します。

したがって、答えはハです。

2018年度　問11

これは公式なので覚えるしかないです。

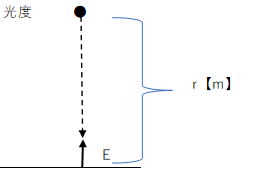
電動機の出力は、E=$\frac{I}{r^2}$ 【lx】 (I：光度【cd】, r：床面上の高さ【m】)

したがって、答えはイです

以上、お疲れさまでした。

「出典：2018年度追加　筆記試験　第1種電気工事士　問1～11:一般財団法人電気技術者試験センター 試験の問題と解答 | ECEE 一般財団法人電気技術者試験センター (shiken.or.jp)　」